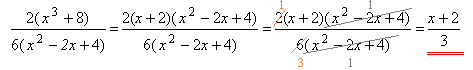Для того, щоб скоротити алгебраїчний дріб, потрібно чисельник і знаменник розкласти на множники. Якщо виявиться, що чисельник і знаменник мають спільні множники, їх можна скоротити.
Прийоми розкладання многочленів на множники:
- винесення спільного множника за дужки;
- використання тотожностей скороченого множення;
- спосіб групування.
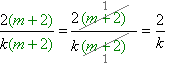 | дріб скорочений на двочлен \((m + 2)\); |
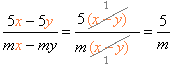 | чисельник і знаменник дробу розкладені на множники, дріб скорочений на спільний множник \((x – y)\); |
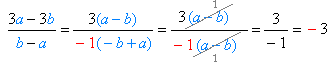 | чисельник і знаменник дробу розкладені на множники, дріб скорочений на \((a - b)\); |
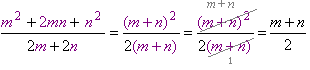 | чисельник дробу розкладений на множники за допомогою формули квадрата суми; у знаменнику спільний множник винесено за дужки; дріб скорочений на спільний множник \((m + n)\). |
Тотожності скороченого множення, які можна використовувати при скороченні дробів
Квадрат суми: ;
Квадрат різниці: ;
Сума кубів: ;
Різниця кубів: .
Приклад:
Скороти дріб: .
Розв'язання:
1. Чисельник і знаменник дробу розкладаємо на множники, використовуючи формули різниці квадратів і квадрата різниці.
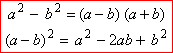 |
2. Скорочуємо дріб на загальний множник — двочлен \((x-2)\).
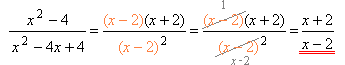
Приклад:
Перетвори дріб таким чином, щоб у знаменнику було .
Розв'язання:
1. Аби зрозуміти, як розширити дріб , вираз розкладаємо на множники.
2. Порівнюємо отриманий вираз зі знаменником дробу \(x + 2\) та робимо висновок, що додатковим множником цього дробу є \(3(x-2)\).
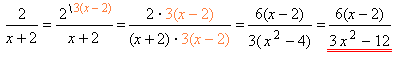
Приклад:
Спрости вираз:
Розв'язання:
1. У чисельнику за дужки виносимо спільний множник \(2\), а в знаменнику — спільний множник \(6\).
2. Вираз розкладаємо на множники, використовуючи формулу суми кубів, а потім дріб скорочуємо.