Ми розглянули функцію для випадку, коли \(k = 1\). Нехай тепер \(k\) — додатне число, відмінне від \(1\), наприклад \(k = 2\).
Розглянемо функцію та складемо таблицю значень цієї функції:
| \(x\) | \(1\) | \(2\) | \(-1\) | \(-2\) | \(4\) | \(-4\) | \(-\) | |
| \(y\) | \(2\) | \(1\) | \(-2\) | \(-1\) | \(4\) | \(-\) | \(-4\) |
Побудуємо ці точки на координатній площині. Вони намічають деяку лінію, що складається з двох гілок. Проведемо її.
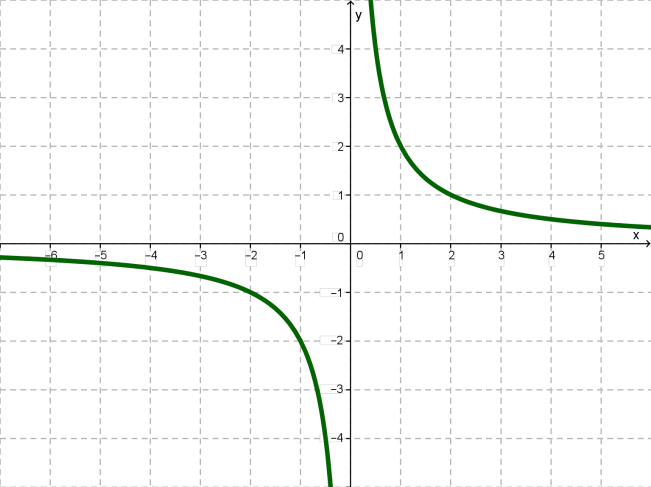
Як і графік функції , ця лінія називається гіперболою.
Тепер розглянемо випадок, коли \(k < 0\); нехай, наприклад, \(k = - 1\).
Побудуємо графік функції (тут \(k = - 1\)).
Графік функції \(y = -f(x)\) симетричний графіку функції \(y = f (x)\) щодо осі \(x\).
Зокрема, це означає, що графік функції \(y = - f (x)\) симетричний графіку функції \(y = f (x)\) щодо осі \(x\).
Отже, графік функції симетричний графіку відносно осі абсцис.
У такий спосіб ми отримаємо гіперболу, гілки якої розташовані в другому і четвертому координатних кутах.
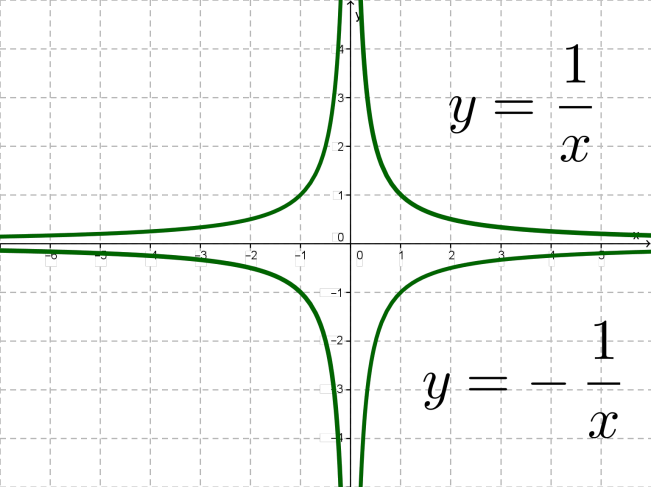
Взагалі, графіком функції , є гіпербола, гілки якої розташовані в першому і третьому координатних кутах, якщо \(k > 0\), і в другому та четвертому координатних кутах, якщо \(k < 0\).
Точка \((0; 0)\) — центр симетрії гіперболи, осі координат — асимптоти гіперболи.
Зазвичай кажуть, що дві величини \(x\) і \(y\) обернено пропорційні, якщо вони пов'язані співвідношенням \(xy = k\) (де \(k\) — число, відмінне від \(0\)) або, що те ж саме, .
З цієї причини функцію називають іноді оберненою пропорційністю (за аналогією з функцією \(y = kx\), яку називають прямою пропорційністю).
Число \(k\) — коефіцієнт оберненої пропорційності.
Властивості функції , якщо \(k > 0\)
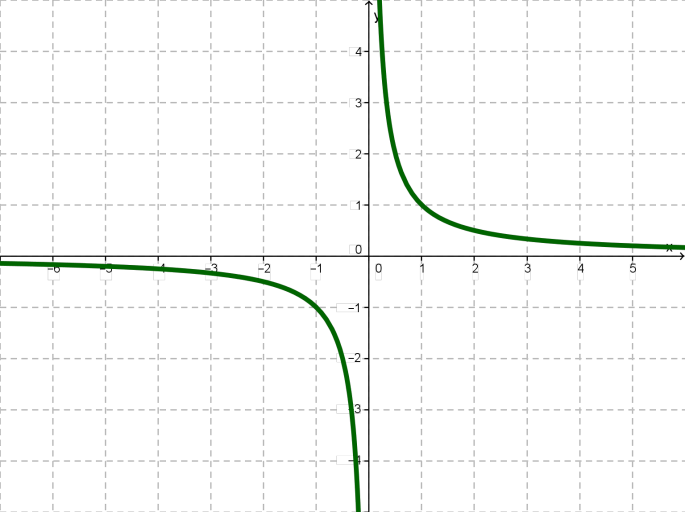
1. Область визначення функції складається зі всіх чисел, окрім \(x = 0\).
2. \(y > 0\), якщо \(x > 0\); \(y < 0\), якщо \(x < 0\).
3. Функція спадає на проміжках .
4. Функція необмежена ні знизу, ні зверху.
5. Функція не має ні найменшого, ні найбільшого значення.
6. Функція неперервна на проміжках і зазнає розриву, якщо \(x = 0\).
7. Область значень — об'єднання двох відкритих променів .
Властивості функції , якщо \(k < 0\)
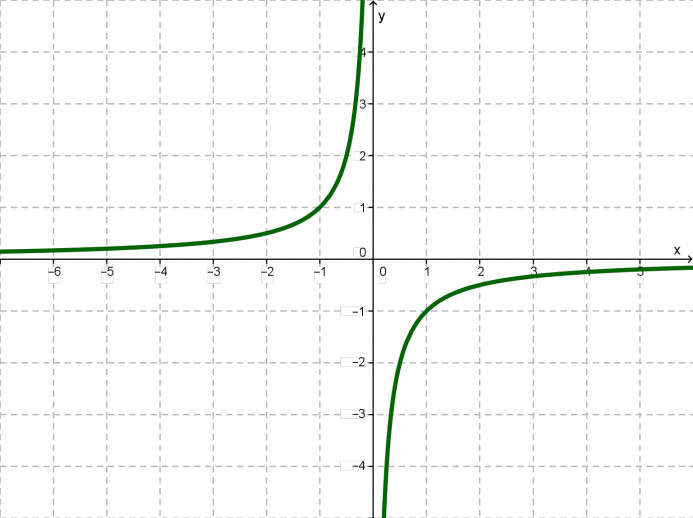
1. Область визначення функції складається зі всіх чисел, окрім \(x = 0\).
2. \(y > 0\), якщо \(x < 0\); \(y < 0\), якщо \(x > 0\).
3. Функція зростає на проміжках .
4. Функція необмежена ні знизу, ні зверху.
5. Функція не має ні найменшого, ні найбільшого значення.
6. Функція неперервна на проміжках і зазнає розриву, якщо \(x = 0\).
7. Область значень — об'єднання двох відкритих променів .