2. Ступенева функція з парним і непарним натуральним показником ступеня

Функція

y = x^{2 n}

Мова йде про функції

y = x^{6}, y = x^{8}

і взагалі про степеневу функцію з парним натуральним показником ступеня. Графік будь-якої такої функції схожий на графік функції

y = x^{4}

, тільки його гілки більш круто спрямовані вгору.

Відзначимо ще, що крива

y = x^{2 n}

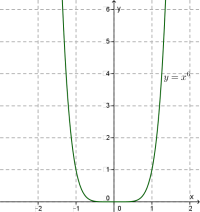
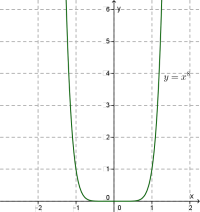
торкається осі \(x\) в точці \((0;0)\). Геометрично це означає, що одна гілка кривої плавно переходить в іншу, як би притискаючись до осі \(x\).

Функція

y = x^{2 n + 1}

Мова йде про функції

y = x^{5}, y = x^{7}, y = x^{9}

і взагалі про степеневу функцію з непарним натуральним показником ступеня. Графік будь-якої такої функції схожий на графік функції

y = x^{3}

, тільки чим більше показник, тим більш круто спрямовані вгору і відповідно вниз гілки графіка. Відзначимо ще, що крива

y = x^{2 n + 1}

торкається осі \(x\) в точці \((0;0)\).

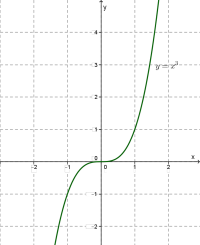
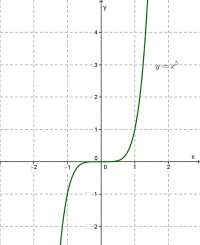
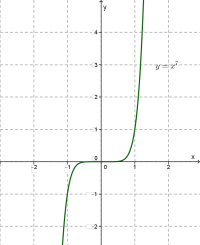
Приклад:

Вирішити рівняння

x^{5} = 3 - 2 x

1. Розглянемо дві функції

y = x^{5}, y = 3 - 2 x

2. Побудуємо графік функції

y = x^{5}

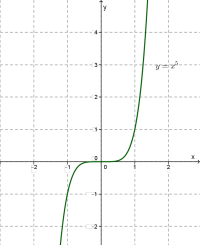
3. Побудуємо графік лінійної функції

y = 3 - 2 x

. Це пряма лінія, що проходить через точки \((0;3)\) та \((1;1)\).

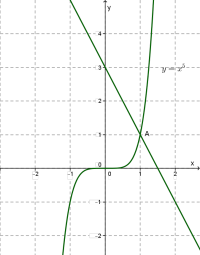
4. Судячи з кресленням, побудовані графіки перетинаються в точці \(A\)\((1;1)\). Перевірка показує, що насправді координати точки \(A\)\((1;1)\) задовольняють і рівнянню