Припустимо, що на площині \(xОy\) дано фігуру, яку обмежує пряма \(Ox,\) прямі \(x=a,\) \(x=b\) і графік невід'ємної функції \(f(x)\) на проміжку\([a,b].\)
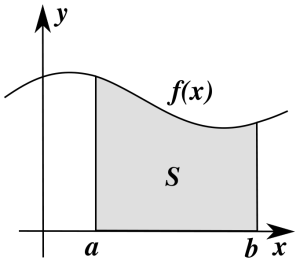
Площу цієї фігури можна обчислити, використовуючи формулу \(,\) де \(F(x)\) є первісною функції \(f(x),\) тобто \(.\)
Приклад:
1) Обчисли площу фігури, обмеженої графіком функції на проміжку \([1,2].\)
Розв'язання
Для функції однією з первісних є функція . Тоді шукана площа
2) Обчисли площу фігури, обмеженої графіком функції на проміжку \([1,2].\)
Розв'язання
Спочатку знаходиться первісна даної функції (використовується метод інтегрування частинами).
Отже:
первісна функції — \(;\)
значення площі — \(.\)