Якщо подається якийсь раціональний вираз \(A\), то, помноживши його на \(-1\), отримуємо .
Два раціональних вирази \(A\) і \(-A\) називаються взаємно протилежними раціональними виразами, якщо їх сума дорівнює \(0\), тобто 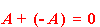 .
.
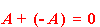 .
.Протилежні вирази, так само, як і протилежні числа, відрізняються один від одного лише знаком.
Наступні вирази є взаємно протилежними:
- \(5\) і \(-5\);
- \(а+b\) і\( -a-b\);
- \(x/y\) і \(-x/y\);
- \(m²-m+3\) і \(-m²+m-3.\)
Це так, оскільки:
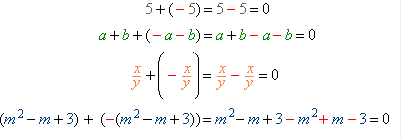
Вирази \(m²-m+3\) та \(-m²+m-3\) — це взаємно протилежні многочлени.
Виконуючи дії з дробовими раціональними виразами, чисельник і знаменник певного дробу досить часто доводиться змінювати на протилежний вираз.
Але, щоб значення дробу не змінилося, потрібно дотримуватися закону зміни знаків. Він полягає в тому, що значення дробу не зміниться, якщо змінити знаки на протилежні:
- у чисельника та знаменника дробу;
- у чисельника та всього дробу;
- у знаменника та всього дробу.
Якщо літерами \(A\) і \(B\) позначимо чисельник і знаменник раціонального виразу, закон зміни знаків можна записати таким чином:
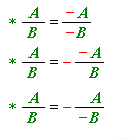
Цей закон діє лише тоді, коли 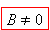 .
.
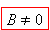 .
.| 1) | 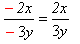 | змінено знаки в чисельнику та знаменнику; |
| 2) | 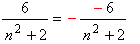 | змінено знак у чисельнику та перед дробом; |
| 3) | 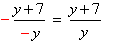 | змінено знак у знаменнику та перед дробом. |
У правильності кожної рівності можна переконатися, вибравши будь-яке значення змінної з області визначення дробу.
Перетворення є правильним за всіх значень \(m\), окрім \(m=0\).
Перевіримо це, якщо \(m=1\) та якщо \(m=10\)
Якщо \(m=1\), тоді
Якщо \(m=10\), тоді