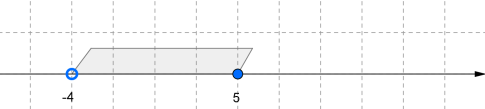
Якщо число \(x\) є розв'язком як нерівності \(x>-4\), так і нерівності \(х<5\), тоді воно є розв'язком подвійної нерівності \(-4<x<5\).
Множину усіх чисел, що задовільняють подвійній нерівності \(-4<x<5\) називають числовим проміжком і позначають: \((-4;5)\).
Зобразимо проміжок на малюнку. Точки малюємо виколотими, оскільки вони не належать проміжку.
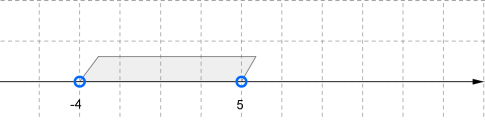
Розглянемо інші проміжки.
або . Читається: «Проміжок від \(-4\) до \(5\), включаючи \(-4\) та \(5\)».
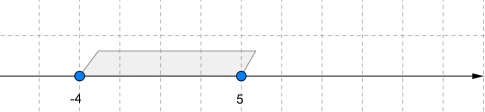
або . Читається: «Проміжок від \(-4\) до \(5\), включаючи \(-4\)».
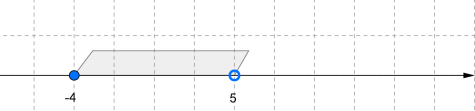
або . Читається: «Проміжок від \(-4\) до \(5\), включаючи \(5\)».