На вільній поверхні рідини молекули перебувають в особливих умовах, які відрізняються від умов, у яких перебувають молекули всередині рідини.
Розглянемо дві молекули — А і Б: молекула А перебуває всередині рідини, а молекула Б — на її поверхні. Молекула А оточена іншими молекулами рідини рівномірно, тому сили, що діють на молекулу А з боку молекул, які потрапляють у сферу міжмолекулярної взаємодії, скомпенсовані, тобто їх рівнодійна дорівнює нулю.
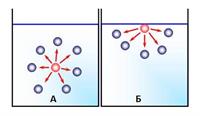
Молекула Б з одного боку оточена молекулами рідини, а з другого боку — молекулами газу. Оскільки з рідини на неї діє набагато більше молекул, ніж із газу, то рівнодійна \(F\) міжмолекулярних сил напрямлена вглиб рідини. Щоб молекула з глибини рідини потрапила в поверхневий шар, потрібно виконати роботу проти нескомпенсованих міжмолекулярних сил. Це означає, що молекули поверхневого шару рідини (порівняно з молекулами всередині рідини) мають надлишкову потенціальну енергію. Ця надлишкова енергія є складником внутрішньої енергії рідини і називається поверхневою енергією (Wпов).
Очевидно, що чим більшою є площа \(S\) поверхні рідини, тим більша поверхнева енергія: , де σ (сигма) — коефіцієнт пропорційності, який називають поверхневим натягом рідини.
Поверхневий натяг рідини — фізична величина, яка характеризує дану рідину і дорівнює відношенню поверхневої енергії до площі поверхні рідини: .
Зверни увагу!
Одиниця поверхневого натягу в СІ —ньютон на метр:
Поверхневий натяг рідини визначається силами міжмолекулярної взаємодії, тому він залежить:
- від природи рідини: у летких рідин (ефір, спирт, бензин) поверхневий натяг менший, ніж у нелетких (ртуть, рідкі метали);
- від температури рідини: чим вища температура рідини, тим меншим є поверхневий натяг рідини;
- від наявності в складі рідини поверхнево активних речовин; їх наявність значно зменшує поверхневий натяг рідини;
- від властивостей газу, з яким рідина межує.
У таблицях зазвичай наводять значення поверхневого натягу на межі рідини і повітря за певної температури.
Коефіцієнт поверхневого натягу рідин (при \(20°C\))
| Рідина | |
|
Бензин
|
21 |
| Спирт | 22 |
| Гас | 24 |
| Нафта | 30 |
| Мильний розчин | 40 |
| Молоко | 46 |
| Вода | 73 |
| Ртуть | 510 |
Оскільки поверхневий шар рідини має надлишкову потенціальну енергію, а будь-яка система прагне до мінімуму потенціальної енергії, то вільна поверхня рідини прагне зменшити свою площу (скоротитися). Тобто вздовж поверхні рідини діють сили, що намагаються стягнути цю поверхню. Ці сили називають силами поверхневого натягу. Наявність сил поверхневого натягу робить поверхню рідини схожою на розтягнуту гумову плівку, однак пружні сили в гумовій плівці залежать від площі її поверхні (тобто від того, наскільки плівка деформована), а поверхня рідини завжди «натягнута» однаково, тобто сили поверхневого натягу не залежать від площі поверхні рідини. Існування сил поверхневого натягу можна експериментально довести за допомогою такого досліду. Якщо дротяний каркас із прив’язаною до нього ниткою занурити в мильний розчин, каркас затягнеться мильною плівкою, а нитка набере довільної форми. Якщо ж обережно проткнути голкою мильну плівку з одного боку від нитки, сила поверхневого натягу мильного розчину, яка діє з іншого боку нитки, натягне нитку.
Опустимо в мильний розчин дротяну рамку, одна зі сторін якої рухома. На рамці утвориться мильна плівка. Будемо розтягувати цю плівку, діючи на поперечину (рухому сторону рамки) з певною силою . Якщо під дією цієї сили поперечина переміститься на \(∆x\) , то зовнішні сили виконають роботу:
За рахунок виконання цієї роботи площі обох поверхонь плівки збільшаться, а отже, збільшиться й поверхнева енергія:
Прирівнявши праві частини рівнянь отримаємо формулу для визначення сили поверхневого натягу:
У повсякденному житті ви постійно зустрічаєтеся з проявами сил поверхневого натягу. Так, завдяки йому на поверхні води утримуються легкі предмети і деякі комахи.

Коли ви купаєтесь і пірнаєте у воду з головою, ваше волосся розходиться в усі боки, але щойно виринете з води, як волосся злипається, бо в цьому випадку площа вільної поверхні води набагато менша, ніж у разі окремого розташування кожного пасма. З цієї ж причини можна побудувати різні фігури з вологого піску: вода, обволікаючи піщинки, притискає їх одну до одної.
Прагненням рідини зменшити площу поверхні пояснюється й той факт, що в умовах невагомості вода набуває форми кулі, — за даного об’єму кулястій формі відповідає найменша площа поверхні. Форми кулі набувають і тонкі мильні плівки (мильні бульбашки). Поверхневим натягом пояснюється утворення піни: бульбашка газу, досягнувши поверхні рідини, утворює над собою тонкий шар рідини; якщо бульбашка мала, то архімедової сили недостатньо, щоб розірвати подвійний поверхневий шар, і бульбашка застрягає поблизу поверхні.
Завдяки поверхневому натягу рідина не виливається з маленького отвору тонесеньким струменем, а капає, дощ не проливається через тканину парасолі або намету тощо.

Наявність сил поверхневого натягу виявляється у сферичній формі дрібних крапельок роси, у краплях води, що розбігаються по розпеченій плиті,у крапельках ртуті на поверхні скла. Однак у випадку зіткнення з твердим тілом сферична форма краплі здебільшого не зберігається. Форма вільної поверхні рідини залежить від сил взаємодії молекул рідини з молекулами твердого тіла. Якщо сили взаємодії між молекулами рідини більші, ніж сили взаємодії між молекулами рідини та твердого тіла, рідина не змочує поверхню твердого тіла. Наприклад, ртуть не змочує скло, а вода не змочує вкриту сажею поверхню. Якщо ж крапельку ртуті помістити на цинкову пластинку, то крапелька прагнутиме розтектися по поверхні пластинки; так само поводиться й крапелька води на склі. Якщо сили взаємодії між молекулами рідини менші від сил взаємодії між молекулами рідини і твердого тіла, рідина змочує поверхню твердого тіла.

У природі часто зустрічаються тіла, пронизані численними дрібними капілярами (від латин. capillaris — волосяний) — вузькими каналами довільної форми. Таку структуру мають папір, дерево, ґрунт, багато тканин і будівельних матеріалів. У циліндричних капілярах скривлена поверхня рідини являє собою частину сфери, яку називають меніском. У змочувальній рідині утворюється ввігнутий меніск, а в незмочувальній — опуклий. Поверхня рідини прагне до мінімуму потенціальної енергії, а викривлена поверхня має більшу площу порівняно з площею перерізу капіляра, тому поверхня рідини прагне вирівнятись і під нею виникає надлишковий (від’ємний або додатний) тиск — тиск Лапласа. Під увігнутою поверхнею (рідина змочує капіляр) загальний тиск менший від тиску на поверхню рідини й рідина втягується в капіляр, піднімаючись на досить велику висоту. Так піднімаються волога та поживні речовини в стеблах рослин, гас у ґноті, волога у ґрунтових капілярах. Унаслідок капілярного тиску серветки або тканина вбирають воду, штани в дощову погоду сильно намокають знизу тощо. Під опуклою поверхнею (рідина не змочує капіляр) тиск більший за зовнішній тиск і рідина в капілярі опускається. Чим меншим є радіус капіляра, тим більша висота підняття (або опускання) рідини.
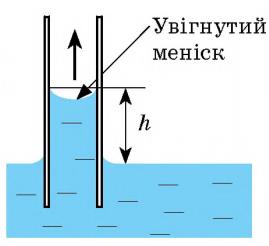
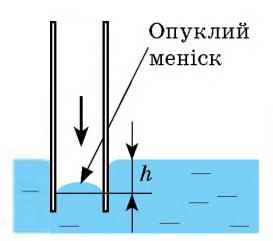
Далі покажемо від чого саме залежить висота рідини в капілярі. Розглянемо ситуацію коли рідина піднялась максимально по капіляру і подивимось, які сили діють на стовбчик рідини в ньому.
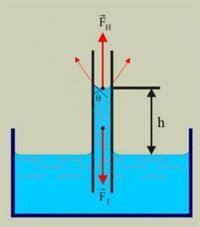
Як бачимо, сила поверхневого натягу зрівноважена силою тяжіння. Розпишемо відповідну рівність і виведемо формулу залежності висоти рідини в круглому капілярі:
Зверни увагу!
Розпишемо масу і довжину контуру капіляру. Рідина в капілярі має форму циліндра а контур має форму круга.
Таким чином висота на яку піднімається данна рідина залежить від її поверхневого натягу й радіуса капіляру. Це справедливо лише для циліндричного капіляру, для капілярів інших форм формула буде іншою!
Джерела:
Фізика (рівень стандарту, за навчальною програмою авторського колективу під керівництвом Локтєва В. М.) : підруч. для 10 кл. закл. загал. серед. освіти / [В. Г. Бар’яхтар, С. О. Дов гий, Ф. Я. Божинова, О. О. Кірюхіна] ; за ред. В. Г. Бар’яхтара, С. О. Довгого. — Харків : Вид-во «Ранок», 2018. — 272 c. : іл.
