Якщо на дорозі сталася аварія, і фахівці вимірюють гальмівний шлях, то для чого вони це роблять? (ці дані потім використовують для з’ясування причини аварії).
Як, знаючи час гальмування й гальмівний шлях, визначити швидкість і прискорення руху тіла?
Як, знаючи час гальмування й гальмівний шлях, визначити швидкість і прискорення руху тіла?
Ми вже знаємо:
Для будь-якого руху проекція переміщення чисельно дорівнює площі фігури під графіком залежності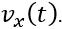 
.
.
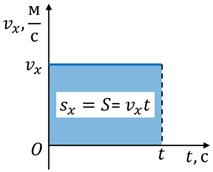
Розглянемо рівноприскорений рух, за якого початкова швидкість і прискорення мають однаковий напрямок із віссю OX.
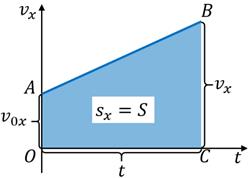
Проекція переміщення чисельно дорівнює площі трапеції OABC:
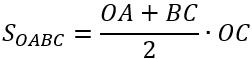
Замінивши зазначені відрізки відповідними фізичними величинами, отримаємо формулу для визначення проекції переміщення:
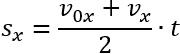\((1)\)Підставивши в цю формулу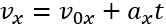 
, отримаємо:
, отримаємо:
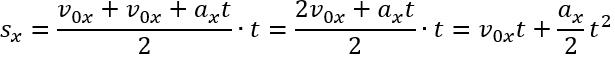
Рівняння проекції переміщення:
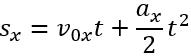\((\)\(2)\)Графік проекції переміщення в разі рівноприскореного прямолінійного руху — парабола.
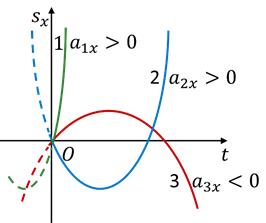
Якщо
, то вітки параболи напрямлені вгору (графіки \(1, 2\)).Якщо
, то вітки параболи напрямлені вниз (графік \(3\)).Чим крутіше графік, тим більше прискорення (
)Скориставшись означенням прискорення та формулою\( (1)\), можна отримати ще одну формулу для обчислення переміщення.
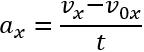
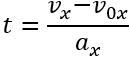
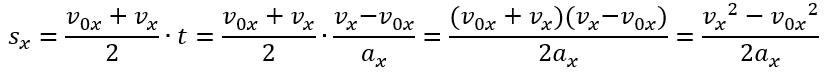
Отже,
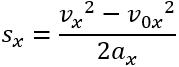
Розглянемо рисунок:
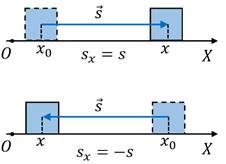
Із рисунку бачимо, що незалежно від напрямку руху координату x тіла можна визначити за формулою:
, де
— початкова координата (координата тіла в момент початку спостереження);
— проекція переміщення.Для рівноприскореного руху
Рівняння координати для рівноприскореного прямолінійного руху:
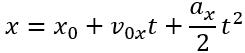
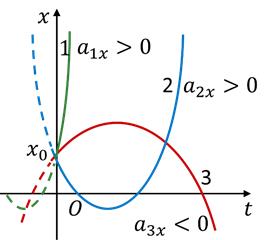
Проаналізувавши останнє рівняння, доходимо висновку, що залежність \(x(t)\) є квадратичною, тому графік координати — парабола.
Джерела:
1. Фізика : підруч. для 9 кл. загальноосвіт. навч. закл. / [В. Г. Бар’яхтар С. О. Довгий, Ф. Я. Божинова, О. О. Кірюхіна] ; за ред. В. Г. Бар’яхтара С. О. Довгого. — Харків : Вид-во «Ранок», 2017. — 272 с. : іл., фот.
2. Фізика : підруч. для 9-го кл. загальноосвіт. навч. закл. / В.Д. Сиротюк. — Київ : Генеза, 2017. — 248 с. : іл.
3. Фізика : підруч. для 9 кл. загальноосвіт. навч. закладів / Т. М. Засєкіна, Д. О. Засєкін. — К. : УОВЦ «Оріон», 2017. — 272 с. : іл.
2. Фізика : підруч. для 9-го кл. загальноосвіт. навч. закл. / В.Д. Сиротюк. — Київ : Генеза, 2017. — 248 с. : іл.
3. Фізика : підруч. для 9 кл. загальноосвіт. навч. закладів / Т. М. Засєкіна, Д. О. Засєкін. — К. : УОВЦ «Оріон», 2017. — 272 с. : іл.
4. https://www.fizikanova.com.ua