Циліндр — це тіло обертання, отримане при обертанні прямокутника навколо його сторони.
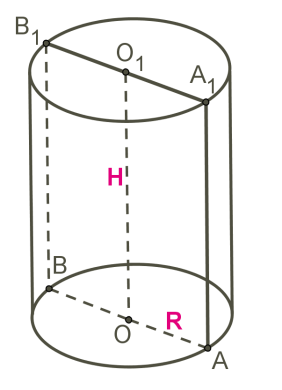
Прямокутник обертається навколо сторони .
— вісь симетрії циліндра і висота циліндра.
— твірна циліндра, довжина якої дорівнює довжині висоти циліндра.
\(AO\) — радіус циліндра.
— вісь симетрії циліндра і висота циліндра.
— твірна циліндра, довжина якої дорівнює довжині висоти циліндра.
\(AO\) — радіус циліндра.
Отримана циліндрична поверхня називається бічною поверхнею циліндра, а круги — основами циліндра.
Осьовий переріз циліндра — це перетин циліндра площиною, яка проходить через вісь циліндра. Цей переріз є прямокутником.
При перерізі циліндра площиною, паралельною осі циліндра (тобто перпендикулярною основі), також виходить прямокутник.
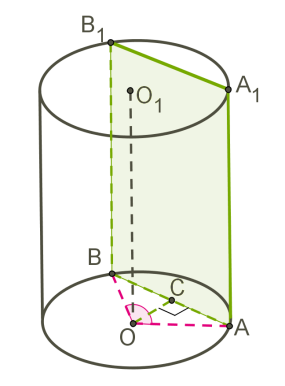
На малюнку зображений циліндр, перетнутий площиною, яка паралельна осі циліндра .
— прямокутник.
\(OA = ОB = R\) — радіуси.
\(OA = ОB = R\) — радіуси.
\(OC\) — відстань від осі циліндра до площини перерізу.
Дуга \(AB\) дорівнює центральному куту \(AOB\).
Дуга \(AB\) дорівнює центральному куту \(AOB\).
При перерізі циліндра площиною, паралельною основі, в перерізі отримуємо коло, що дорівнює основам циліндра.
Якщо уявити, що бічна циліндрична поверхня розрізана по твірній і розгорнута, отримаємо прямокутник.

Сторона дорівнює висоті \(H\), а іншу сторону утворює розгорнуте коло основи довжиною .
Оскільки розгортка — прямокутник, тоді бічна поверхня визначається за формулою:
Основи циліндра — два круги із загальною площею .
Повна поверхня циліндра визначається за формулою: