Рівність трикутників
Якщо два трикутники, які можна сумістити за допомогою накладання, називають рівними.
При накладанні трикутників збігаються всі сторони та всі кути.
Якщо два трикутники рівні, то елементи (сторони й кути) одного трикутника відповідно дорівнюють елементам другого трикутника.
Розглянемо рівні трикутники \(і\) \(.\)
В результаті накладання відповідно сумістяться сторони й кути цих трикутників, тобто кожному елементу трикутника відповідатиме рівний елемент трикутника \(.\)
В результаті накладання відповідно сумістяться сторони й кути цих трикутників, тобто кожному елементу трикутника відповідатиме рівний елемент трикутника \(.\)
Зверни увагу!
В записі назви трикутників впорядковуються так, щоб вершини рівних кутів зазначалися в порядку відповідності. Це означає, що якщо:
\(=\) \(,\) то справджуються шість рівностей відповідних елементів: три — для кутів і три — для сторін.
\(=\) \(,\) то справджуються шість рівностей відповідних елементів: три — для кутів і три — для сторін.
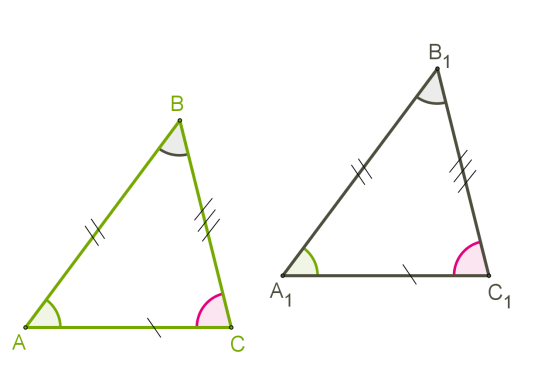
На рисунках відповідно рівні сторони зазвичай позначають однаковою кількістю рисок, а відповідно рівні кути — однаковою кількістю дужок.
На практиці не завжди можна застосувати спосіб накладання для порівняння фігур. Найчастіше необхідно обмежитися виміром деяких елементів фігур, і за цими вимірами робити висновок про їхню рівність.