3. Застосування другої ознаки рівності трикутників

У рівнобедреному трикутнику \(ABC\) з основою \(AC = \) 5 \(cм\) проведено бісектрису кута $\angle \mathit{ABC}$ Використовуючи другу ознаку рівності трикутників, доведи, що відрізок \(BD\) є медіаною, визнач довжину відрізка \(AD.\)

 

 

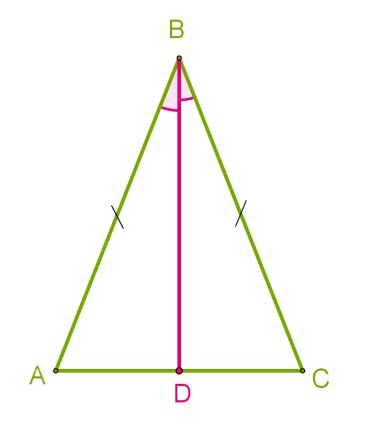
\(1.\) $\angle$$A$ \(=\) $\angle$\(,\) кути рівнобедреного трикутника прилеглі до основи.

 

\(2.\) $\angle$ \(=\) $\angle$$\mathit{CBD}$\(,\) за властивістю бісектриси.

 

\(3.\) Сторони \(AB = CB\) у $\mathrm{\Delta }$$\mathit{ABD}$ та $\mathrm{\Delta }$$\mathit{CBD}$ рівні, оскільки $\mathrm{\Delta }$\(ABC\) — \(.\)

 

За другою ознакою рівності трикутників $\mathrm{\Delta }$$\mathit{ABD}$ та $\mathrm{\Delta }$$\mathit{CBD}$ рівні.

 

Отже, у рівних трикутників рівними є відповідні елементи, то \(AD = CD.\) Це означає, що відрізок \(BD\) ділить сторону \(AC\) навпіл, тобто є медіаною даного трикутника.

 

\(AD\) =  \(см\)