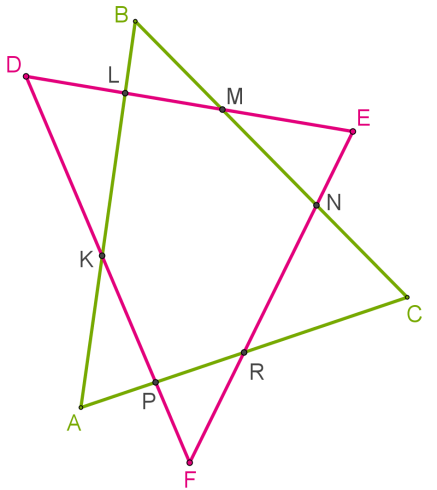
Периметр трикутника \(ABC\) дорівнює 5 \(см,\) периметр трикутника \(DEF\) — 7 \(см.\)
Доведи, що периметр шестикутника \(PKLMNR\) менший, ніж 6 \(см.\)
\(1.\) Розглянь трикутники \(PAK,\) \(KDL,\) \(LBM,\) \(MEN,\) \(NCR\) і \(RFP.\)
Напиши для кожного з них нерівність трикутника для сторін, які також є сторонами шестикутника.
\(PK\) \(<\) \(PA\) \(+\)
\(KL\) \(<\) \(+\)
\(<\) \(+\)
\(<\) \(+\)
\(<\) \(+\)
\(<\) \(+\)
\(2.\) Якщо додати праві та ліві сторони правильних нерівностей, отримаємо правильну нерівність.
Яку з величин отримаємо в лівій стороні після додавання?
\(3.\) Якщо до обох сторін правильної нерівності додати одну й ту саму величину, отримаємо правильну нерівність. Додай до обох сторін отриманої в попередньому кроці правильної нерівності \(PK + KL + LM + MN + NR + RP.\)
Які з величин отримаємо в лівій стороні після додавання?
\(4.\) Які з величин отримаємо в правій стороні після додавання?
\(5.\) Чому дорівнює права сторона отриманої нерівності, якщо використовувати дані числові значення?
Відповідь:
\(6.\) Що необхідно зробити з обома сторонами отриманої нерівності, аби довести, що периметр шестикутника \(PKLMNR\) менший, ніж 6 \(см?\)
Ви повинні авторизуватися, щоб відповісти на завдання. Будь ласка, увійдіть в свій профіль на сайті або зареєструйтеся.