Якщо всі сторони чотирикутника дотикаються до кола, то він називається чотирикутником, описаним навколо кола, а коло — вписаним у чотирикутник.
Не всі чотирикутники можливо описати навколо кола, оскільки бісектриси чотирьох кутів можуть не перетинатися в одній точці. У такому випадку не вдасться знайти центр вписаного кола.
Суми протилежних сторін описаного чотирикутника дорівнюють \(a+c=b+d.\)
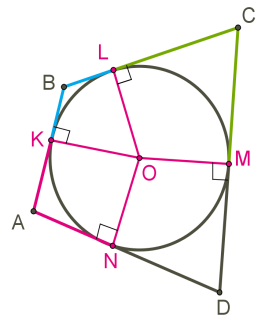
Оскільки відрізки дотичних, проведених із однієї точки до кола, рівні, і \(AB = AK + KB,\) \(BC = BL + LC,\) \(CD = CM + MD\) та \(AD = DN + NA,\) то \(AB + CD = BC + AD.\)
Цю властивість можна використовувати і як ознаку для визначення того, в які чотирикутники можна вписати коло.
Якщо суми протилежних сторін чотирикутника рівні, то в такий чотирикутник можна вписати коло.
Самостійно зроби огляд чотирикутників (паралелограма, зокрема квадрата, прямокутника, ромба, рівнобедреної і прямокутної трапецій), у які можна вписати коло.