Чотирикутник, усі вершини якого лежать на колі, називається вписаним у коло, а коло називається описаним навколо чотирикутника.
Не всі чотирикутники можна вписати в коло, оскільки серединні перпендикуляри чотирьох сторін можуть не перетинатися в одній точці. У такому випадку не вдасться знайти центр кола, описаного навколо чотирикутника.
Сума протилежних кутів вписаного чотирикутника дорівнює \(180\) градусам.
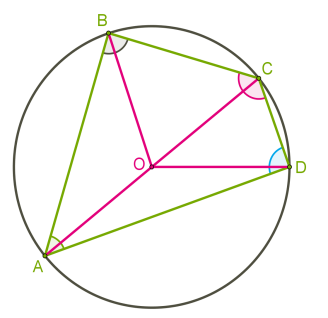
Усі кути чотирикутника є вписаними в коло, отже, дорівнюють половині дуг, на які спираються. Протилежні кути спираються на дуги, які разом утворюють коло, тобто \(.\) Отже, протилежні кути разом складають \(.\)
Цю властивість можна використовувати і як ознаку для визначення того, навколо яких чотирикутників можна описати коло.
Якщо сума протилежних кутів чотирикутника дорівнює \(180\)\(,\) то навколо нього можна описати коло.
Самостійно зроби огляд чотирикутників (паралелограма, зокрема квадрата, прямокутника, ромба, рівнобедреної і прямокутної трапецій), навколо яких можна описати коло.