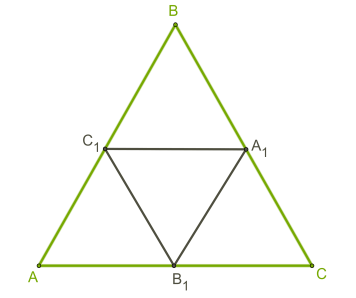
На малюнку зображено правильний трикутник \(ABC.\) Позначено та з'єднано серединні точки всіх сторін. Припустимо, що для трикутника знову повторили той самий процес, і так \(n\) разів.
Визнач площу трикутника \(,\) якщо сторона трикутника \(ABC\) дорівнює \((од. вим.). \)
\( \)
\( \)
Відповідь:
Ви повинні авторизуватися, щоб відповісти на завдання. Будь ласка, увійдіть в свій профіль на сайті або зареєструйтеся.