Висловлювання— це твердження про певний об’єкт або про зв’язки між об’єктами і про яке можна однозначно сказати, істинне воно чи хибне.
Основною властивістю висловлювання є його істинність. Якщо висловлювання істинне, то вважають, що значення його властивості істинність дорівнює True (англ. true — правда). Якщо висловлювання хибне, то вважають, що значення його властивості істинність дорівнює False (англ. false — хиба, хибність).
Висловлювання можна розглядати як логічний вираз.
Логічним виразом називають вираз, який може набувати одне з двох значень: true або false.
Приклад:
Якщо висловлювання істинне, то вважають, що значення відповідного логічного виразу дорівнює True. Тобто, «Київ — столиця України» = True, (2 * 5 - 4 = 6) = True, (4 < 12) = True.
Якщо висловлювання хибне, то вважають, що значення відповідного логічного виразу дорівнює false. Тобто «Це підручник для учнів сьомого класу» = False, (2 * 7 + 3 = 12) = False, (3 > 5) = False.
Змінні логічного типу
Значення логічного виразу можна присвоювати певній змінній.
x = 2 + 12//3 = 6; // х=True
у = 32 < 13; //у=False.
У мові Python для величини, значенням якої є True або False, використовують логічний тип (bool).
Змінні логічного типу також вважаються логічними виразами.
Прості умови
Значень типу bool набувають вирази, побудовані за допомогою операцій порівняння (прості умови):

Логічні вирази набувають значення True або False.
Проаналізуємо результати обчислення логічних виразів:
| >>> print(2*2==4) True | Оскільки 2 · 2 = 4 — істинна рівність, то значення відповідного логічного виразу дорівнює Truе |
| >>> NUM = 10 >>> NUM%3 == 0 False | Отримано відповідь на запитання «Чи ділиться значення змінної NUM на 3?» |
Складені умови
Складений вираз (складена умова) — кілька простих виразів, з’єднаних логічними операціями and (і), or (або), not (ні).
Запереченням логічного виразу x називають логічний вираз, значення якого дорівнює True, якщо значення логічного виразу x дорівнює False, і дорівнює False, якщо значення логічного виразу x дорівнює True.
Заперечення логічного виразу x позначають not x.
Тобто якщо x = True, то not x = False, і якщо x = False, то not x = True.
Тобто якщо x = True, то not x = False, і якщо x = False, то not x = True.
Кон’юнкцієюдвох логічних виразів x і у називають логічний вираз, значення якого є True, якщо значення кожного з логічних виразів x і у є True; і False, якщо значення хоча б одного з логічних виразів x або у є False.
Кон’юнкція двох логічних виразів x і у позначається x and у (англ. and — і, та).
Висловлювання «Число 36 кратне 3 і число 36 кратне 2» є кон’юнкцією двох висловлювань: «Число 36 кратне 3» та «Число 36 кратне 2».
Висловлювання «Число 36 кратне 3 і число 36 кратне 2» є кон’юнкцією двох висловлювань: «Число 36 кратне 3» та «Число 36 кратне 2».
Диз’юнкцією двох логічних виразів x і у називають логічний вираз, значення якого є True, якщо значення хоча б одного з логічних виразів x або у є True; і False, якщо значення кожного з логічних виразів x і у є False.
Диз’юнкція двох логічних виразів x і у позначається x or у (англ. or —або).
Висловлювання «11 ≤ 21» (11 менше або дорівнює 21) є диз’юнкцією двох висловлювань: «11 < 21» та «11 = 21».
Часто використовують логічні вирази, що містять кілька логічних операцій. Наприклад: (x or у) and (x or z).
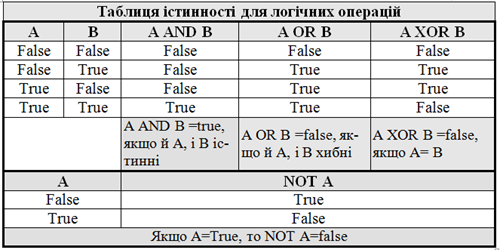
Таблиці істинності
Для обчислення значень логічного виразу можна використати таблицю істинності. У ній потрібно розглянути всі можливі значення змінних логічного типу, що входять до цього виразу.
Таблиця істинності — це прямокутна таблиця, що виражає відповідність між усіма наборами величин змінних і значеннями логічної функції.
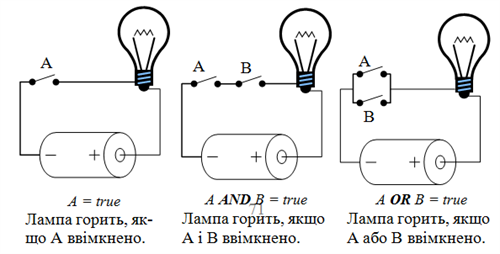
Проілюструємо виконання логічних операцій AND і OR за допомогою електричних схем:
Логічні операції, операції відношення й арифметичні операції можуть зустрічатися в одному виразі. Обчислення таких виразів виконуються зліва направо з урахуванням пріоритету операцій:
1) not; 2) and, *, /, //, %;
3) or, xor, +, –;
4) операції порівняння.
1) not; 2) and, *, /, //, %;
3) or, xor, +, –;
4) операції порівняння.
Приклад:
Розглянемо приклади складених логічних виразів:
а) not (А <= 3) — те саме, що А > 3.
б) (A > 10) and (A < 18) — набуває значення True, якщо значення A належить проміжку від 10 до 18.
в) (A <= 10) or (A >= 18) — набуває значення True, якщо значення A не належить проміжку від 10 до 18.
а) not (А <= 3) — те саме, що А > 3.
б) (A > 10) and (A < 18) — набуває значення True, якщо значення A належить проміжку від 10 до 18.
в) (A <= 10) or (A >= 18) — набуває значення True, якщо значення A не належить проміжку від 10 до 18.
Визначити, чи належить точка з координатою x відрізку [–5; 5].
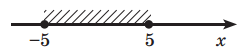
Точка належить відрізку, якщо справджується нерівність –5 ≤ x ≤ 5. У програмуванні таку подвійну нерівність записують як складену умову:
(х >= –5) and (х <= 5).
Приклад:
Обчислити значення логічних виразів:
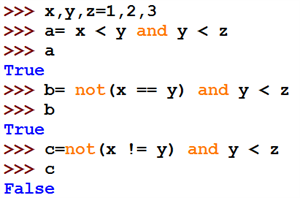
Перетворення типів
Іноді треба перетворювати логічне значення на рядок або число і навпаки. Для цього в мові Python можна застосовувати вбудовані функції перетворення типів:
Вбудовані функції all і any
Одночасну перевірку декількох умов можна записати коротше за допомогою вбудованих функцій all (англ. всі) і any (англ. хоч одна).Функція all(<список логічних виразів>) повертає True, якщо істинні всі перелічені в списку умови.
Приклад:
З’ясуємо, чи є значення NUM парним числом із проміжку від 7 до 20. Для цього слід одночасно перевірити три умови:
>>> NUM = 8
>>> all([NUM >= 7, NUM <= 20, NUM%2 == 0])
True
>>> NUM = 8
>>> all([NUM >= 7, NUM <= 20, NUM%2 == 0])
True
Функція any(<список логічних виразів>) повертає True, якщо хоча б один елемент списку дорівнює True.
Приклад:
Перевіримо, чи дорівнює 0 хоча б одне зі значень x, y, z:
>>> x, y, z = 4, 0, 5
>>> any([x == 0, y == 0, z == 0])
True.
>>> x, y, z = 4, 0, 5
>>> any([x == 0, y == 0, z == 0])
True.
Джерела:
Інформатика : підруч. для 8 кл. закл. заг. серед.освіти / Йосиф Ривкінд [та ін.]. — Київ : Генеза, 2021.
Інформатика :підруч. для 8 кл. закл. заг. серед.освіти / О. О. Бондаренко, В. В. Ластовецький, О. П. Пилипчук, Є. А. Шестопалов. — Х. : Вид-во «Ранок», 2021
