Одиничним квадратом називають квадрат з стороною, що дорівнює одиничному відрізку. Площу такого квадрата визначають як одиницю площі (квадратна одиниця).
 а
аВиміряти площу означає порівняти її з площею одиничного квадрата
Площа фігури дорівнює кількості одиничних квадратів, що укладаються в ній.

рис.\(1\)
Фігура на рис.\(1\) складається з \(7\) одиничних квадратів, тому \(S\) \(=\) \(7\) кв. од.
Властивості площі.
\(1\). Площі рівних фігур є рівними.

рис.\(2\)
Фігури на рис.\(2\) рівні і складаються з однакової кількості одиничних квадратів.
Тоді
\(2\). Якщо фігура розбита на декілька частин, то площа фігури дорівнює сумі площ її частин.
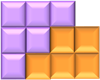
рис.\(3\)
Фігура на рис.\(3\ \)складається з двох частин, фіолетової і жовтогарячої. Фіолетова фігура складається з \(6\) квадратів з стороною \(1\) см і має площу \(6\) см². Жовтогаряча фігура складається з \(5\) квадратів і має площу \(5\) см². Тоді площа фігури \(11\) см².
Прямокутником називається чотирикутник у якого всі кути прямі. Розбивши прямокутник на одиничні квадрати (рис.\(4\)) легко зрозуміти формулу площі прямокутника.

рис.\(4\)
Формула площі прямокутника має вид: , де \(a\) i \(b\) — суміжні сторони прямокутника.
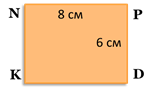
Довжини сторін прямокутника KMPD дорівнюють \(8\) см і \(6\) см. Площа прямокутника буде дорівнювати:
Квадрат — це прямокутник у якого сторони рівні. Тобто суміжні сторони квадрата складаються з однакової кількості одиничних квадратів (рис.5).

рис.\(5\)
Площа квадрата розраховується по формулі:
, де \(a\) — сторона квадрата.

Сторона квадрата \(ABCM\) — \(5\) см. Площа квадрата буде дорівнювати:
Стандартними одиницями вимірювання площі є:
1 см²
1 дм² = 100 см²
1 м² = 100 дм² = 10000 см²
Для вимірювання великих площ використовують інші одиниці вимірювання: ар (а), сотка і гектар (га)
1 а = 100 м²
1 га = 10000 м²
1 км² = 1000000 м²
