Геометрична фігура, яка складається з трьох точок (вершин), які не лежать на одній прямій,
і трьох відрізків (сторін),
що попарно з'єднують ці точки,
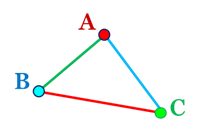
називається трикутником.
Під час запису замість слова "трикутник" використовується знак , а назву трикутника дають за назвами його вершин.
Приклад:
Запис читаємо: "трикутник АВС".
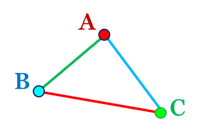
Сторони трикутника: 
Кути трикутника: 
або 
Сума будь-яких двох сторін трикутника більша за третю сторону. І навпаки, якщо сума менших відрізків більша за найбільший відрізок, то із цих трьох відрізків можна скласти трикутник.

Навпроти більшої сторони лежить більший кут.
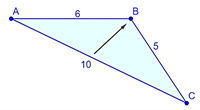
У сторона \(АВ\) \(=\) \(10\) см — найбільша, тоді — найбільший.
Навпроти більшого кута лежить більша сторона.
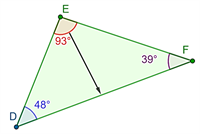
У — найбільший, тоді — найбільша.
Суму довжин усіх сторін трикутника називають його периметром.
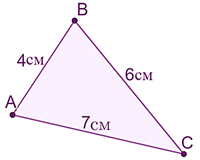
У довжини сторін: \(AB\) \(=\) \(4\) см, \(BC\) \(=\) \(6\) см, \(AC\) \(=\) \(7\) см.
\(4\) \(+\) \(6\) \(+\) \(7\) \(=\) \(17\) (см).