Задачі, в яких умова йде про підрахунок певної кількості варіантів називаються комбінаторними. У них підраховуються різні комбінації заданих об'єктів.
Розділ математики, в якому розглядається розв'язування комбінаторних задач називається комбінаторикою.
Для розв'язання комбіноторних задач використовують правила додавання та множення. Для зручності, доречно користуватись малюнками та схемами.
Нехай об'єкт \(X\) можна вибрати \(a\) спобами, об'єкт \(Y\) вибирати можна \(b\ \)способами, тоді:
- вибір \(X\ або\ Y\) можемо здійснити у \(a + b\ \)способів (правило додавання),
- здійснити вибір \(X\ і\ Y\) можна у \(a · b\) способів (правило множення).
Приклад:
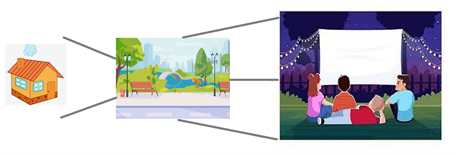
Каринка вирушила назустріч з друзями, що влаштували у місцевому парку "літній кінотеатр". Скільки існує різних маршрутів для дівчинки, якщо до парку від дому є дві пішохідні доріжки, а до друзів парком можна пройти трьома доріжками.
Розглянемо кілька способів розв'язання:
1) Якщо Каринка прямуватиме спочатку шляхом \(a\), то матиме далі можливість скористатись одним з трьох шляхів. Отже, три можливі маршрути. Якщо ж вона обере шлях \(b\), то також три можливі маршрути. Разом \(\)\(\) маршрутів.
2) Від дому до парку ведуть дві дороги, і з парку до кінотеатру три варіанти шляху. Отже, дівчинка митиме \(\)\(\) маршрутів.
Розглянемо графічний спосіб розв'язування комбінаторних задач, такий як "Дерево рішень", або ж "дерево можливих варіантів" , що полягає у перебору варіантів розв'язків задачі.
Приклад:
З чисел 3, 5 та 0 укласти усі можливі трицифрові числа, якщо цифри у записі не мають повторюватись.
Розв'язання:
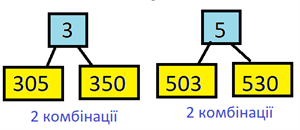
Запишемо цифри та від кожної проведемо стрілочки до комірок, де заповнимо порожні місця у певній послідовності. Відповідно під трійкою матимемо 05 та 50. Отримаємо 305 та 350. Аналогічно для 5-ки. Перераховуємо одержані варіанти. Маємо чотири шуканих трицифрових числа: 350, 305, 530 та 503.
Можна й у наступний спосіб: на перше місце ми можемо поставити лише одну з цифр 3 або 5, наступною одну з двох, що лишились, а для третої варіант розміщення буде єдиний. Отже кількість варіантів трицифрових чисел без повторень це 4.
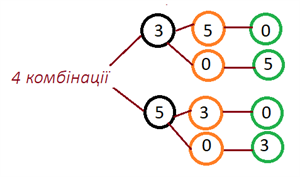
Якщо заміть "0" в умові вказано іншу цифру, то матимемо вже більше комбінацій .
Зверни увагу!
Нуль (0) на початку числа стояти не може.
Зручно подібні завдання виконувати й за допомогою "таблиці варіантів".
Приклад:
Потрібно визначити кількість двоцифрових чисел, утворених за допомогою 0, 3 та 5. Складемо таблицю варіантів, та визначимо кількість можливих значень. Маємо два рядки (можливі десятки) та три стовпці (одиниці).
| Число десятків | Число одиниць | ||
| 0 | 3 | 5 | |
| 3 | 30 | 33 | 35 |
| 5 | 50 | 53 | 55 |
Визначаємо \(2 · 3 = 6\).
Відповідь: \(30, 33, 35, 50, 53, 55\).
Зверни увагу!
Якщо потрібні значення без повторень, то у такій табличці вилучаємо "головну діагональ".
Джерела:
Математика: підручник для 5 класу закладів загальної середньої освіти/ Г.П.Бевз, В.Г.Бевз, Д.В.Васильєва, Н.Г.Владімірова. — К.: Видавничій дім "Освіта", 2022.