У реальному житті в багатьох випадках ми використовуємо два числа (або інші символи), щоб точно описати потрібний нам об'єкт.
Місце в залі задається номером ряду й номером крісла в ряду.

На шаховій дошці позиція фігури задається назвою стовпця та номером ряду.

Будь-яка карта (або глобус) поділена на квадрати, і, подібно до шахівниці, кожен квадрат задається двома номерами.

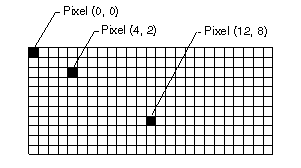
На екрані комп'ютера кожна точка задається двома номерами.
Система координат

Французький філософ і математик Рене Декарт \((1596 - 1650)\) у \(XVII\) \(ст.\) запропонував метод двох координат для знаходження точки на площині. Тому система координат названа його ім'ям.
Декартову систему координат утворюють:
\(1.\) Дві перпендикулярні прямі, на яких зазначено напрям зростання чисел. Горизонтальна пряма називається віссю \(Ox,\) або віссю абсцис. Вертикальна пряма називається віссю \(Oy,\) або віссю ординат.
\(2.\) Точка перетину прямих — початок координатної системи, яка часто позначається буквою \(O.\)
\(3.\) Відрізки на кожній осі завдовжки в одну одиницю вимірювання.
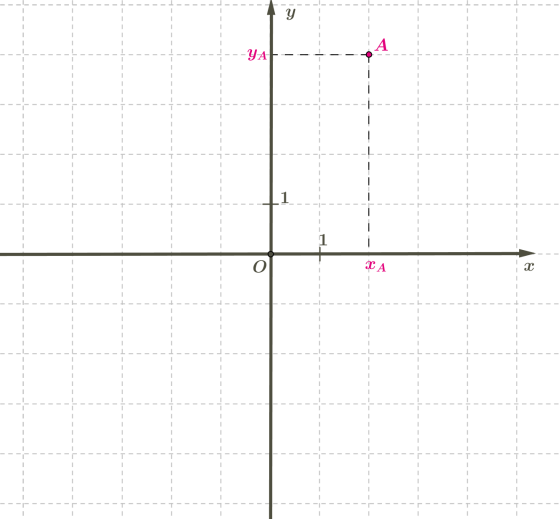

Для будь-якої точки знаходять дві координати \(x\) і \(y\) (абсциссу і ординату) й записують, як \(.\)
На малюнку показано координати \(,\) тобто абсциса точки \(A\) дорівнює \(2,\) а ордината точки \(A\) дорівнює \(4.\)
Якщо на площині вибрано систему координат, то таку площину називають координатною площиною.
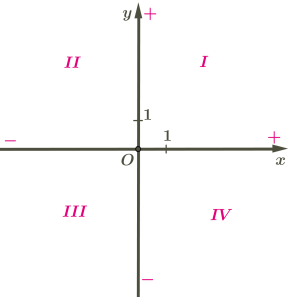
Оскільки осі координат ділять площину на \(4\) частини, кожна з них має номер і називається квадрантом.
У \(I\) чверті розташована додатна частина осі абсцис та осі ординат.
У \(II\) чверті розташована додатна частина осі ординат та від'ємна частина осі абсцис.
У \(III\) чверті розташована від'ємна частина осі абсцис та осі ординат.
У \(IV\) чверті розташована додатна частина осі абсцис та від'ємна частина осі ординат.
У \(II\) чверті розташована додатна частина осі ординат та від'ємна частина осі абсцис.
У \(III\) чверті розташована від'ємна частина осі абсцис та осі ординат.
У \(IV\) чверті розташована додатна частина осі абсцис та від'ємна частина осі ординат.