Дві прямі, що лежать на одній площині, можуть перетинатися в одній точці, або не перетинатися.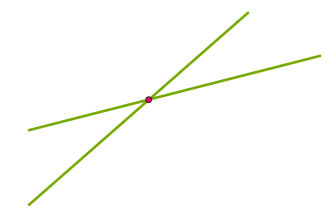



Прямі, які перетинаються - прямі, які мають спільну точку. Цю точку називають точкою перетину.
Якщо прямі лежать на одній площині й не перетинаються, то їх називають паралельними.
Назва походить від грецького слова «паралелос» (παράλληλος), що означає «йдуть поруч».
Чому у визначенні дуже важливо вказати, що ми говоримо про прямі, які лежать на одній площині? Тому що в тому випадку, коли прямі не лежать на одній площині, вони можуть не перетинатися й не бути паралельними, тобто не йти поруч.

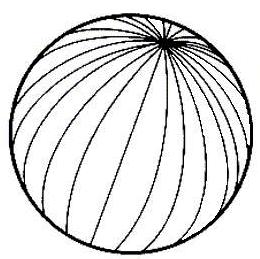
Цікавий приклад отримуємо, розглядаючи прямі на поверхні кулі (не на площині). Якщо куля досить велика, то в певній точці прямі можуть бути паралельними, але насправді вони перетинаються в точках, які називаються полюсами кулі.

Але для прямих, що лежать на одній площині, правильним є те, що точки перетину немає.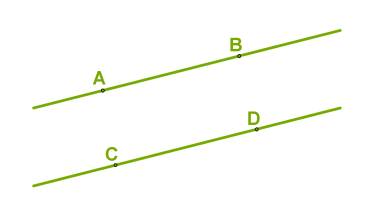

Позначення паралельних прямих: AB || CD
Цей запис читають так: «Пряма AB паралельна прямій CD».
Цей запис читають так: «Пряма AB паралельна прямій CD».
Якщо AB || CD, то CD || AB.
\( \)
Інший спосіб для запису паралельних прямих — a || b.
Інший спосіб для запису паралельних прямих — a || b.
Якщо дві прямі перпендикулярні третій прямій, то вони паралельні. .
Через точку А, що не належить прямій a, можна провести єдину пряму b так, що a || b.
