Площу прямокутника \(ABCD\) можна знайти двома способами.
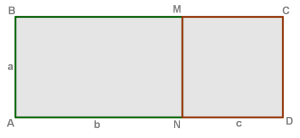
\(1.\) Знайти площу прямокутника \(ABMN,\) площу прямокутника \(MCDN\) і додати їх.
Отримаємо:
\(2.\) Знайти площу прямокутника \(ABCD\) одразу.
Отримаємо:
Отже, правильна рівність:
— розподільний закон множення
На малюнку маємо підтвердження цього закону для випадку, коли \(a, b, c\) — додатні числа.
Але розподільний закон множення виконується для будь-яких чисел.
Приклад:
При застосуванні розподільного закону множення відбувається розкриття дужок і число, що стоїть перед дужками, множиться на кожне число, що стоїть у дужках. Але не завжди перед дужками записаний числовий множник.
Приклад:
\((x-3)\) або \(-(x-3)\)
Якщо перед дужками стоїть знак \(«+»,\) це означає, що всі доданки в дужках потрібно помножити на \(1,\) тобто, розкриваючи дужки, залишити їх без змін.
Якщо перед дужками стоїть знак \(«-»,\) це означає, що всі доданки в дужках потрібно помножити на \(-1,\) тобто, розкриваючи дужки, змінити знаки доданків на протилежні.
Приклад: