Ви вже знайомі з координатною прямою та знаєте, що показує координата точки.
Якщо координата точки відома:
— цю точку можна позначити на координатній прямій;
— модулем координати є відстань від цієї точки до точки О;
— знак координати, вказує напрямок, у якому шукати відстань.
Також, вам вже відомо, як знайти модуль різних раціональних чисел та як розв'язувати рівняння з модулем. Виникає питання, до яких завдань можна застосувати знання?
Накреслимо координатну пряму, узявши за одиничний відрізок 2 клітинки. Позначимо на ній точки: та .
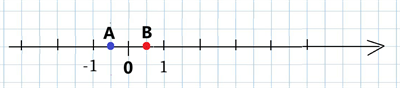
Як бачимо, ці точки рівновіддалені від початку відліку.
Відстань між точками \(A\) і \(B\) — складає один одиничний відрізок, що є сумою відстаней \(AO\) та \(OB\), або сумою відповідних модулів:
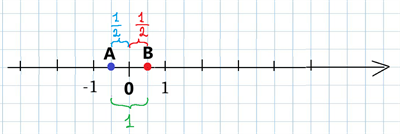
Додамо точку , що знаходиться з точкою \(\)\(\) по різні боки від початку відліку.
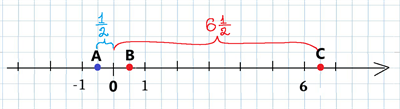
Відстань між точками \(A\) і \(C\), теж є сумою відстаней від точок до початку відліку \(AO\) та \(OC\):
Якщо дано точки \(A(a)\) і \(B(b)\), причому \(a\) — від'ємне, \(b\) — додатне число. Тоді відстань між точками \(A(a)\) і \(B(b)\) на координатній прямій можна знайти як суму модулів:
Знайдемо тепер відстань між точками і :
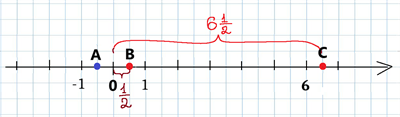
Відстань між точками \(B\) і \(C\), оскільки вони знаходяться по один бік від початку відліку, можна знайти як різницю відстаней \(OC\) та \(OB\):
Якщо дані точки \(A(a)\) і \(B(b)\), мають координати з однаковими знаками, й тобто \(A(a)\) — ближча до \(O\), то на координатній прямій знаходимо різницю модулів:
Приклад:
1) дано точки і , знаходимо відстань між точками:
2) якщо і , відстань між точками:
Також, для знаходження відстаней на координатній прямій можна скористатись узагальненням:
Відстань між точками на координатній прямій дорівнює модулю різниці їх координат:
Джерела:
О. Істер "Математика. Підручник для 6 класу закладів загальної середньої освіти (у 2-х частинах). Частина 2". - Київ "Генеза" - 2023.