Найкоротша відстань між двома точками — це довжина відрізка прямої, що сполучає ці точки.
Ми знаємо, що для вимірювання відрізків використовуються одиниці виміру: .
Дві відстані зручно порівнювати, якщо вони виражені в однакових одиницях вимірювання.
Часто відстань у природі необхідно переносити на схеми, плани, карти. Усі відстані, які переносять на одну й ту саму схему (план, карту), повинні бути порівняні, тобто має бути збережене таке відношення, як у природі.
Приклад:
Якщо в природі одна відстань у \(7\) разів довша, ніж інша, то на схемі ці відстані повинні відрізнятися у \(7\) разів.
Для коректного перенесення відстаней використовують масштаб.
Масштаб — це відношення довжини відрізка на карті до довжини відповідного відрізка на місцевості (у реальності).
Зверни увагу!
Масштаб показує, у скільки разів відстань на карті коротша, ніж відстань на місцевості.
Карту можна використовувати для визначення відстані на місцевості, якщо всі відстані перенесені за одним масштабом.
Які бувають масштаби?
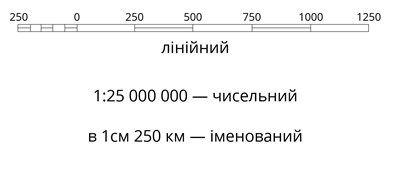
\(1\). Іноді під картою додають лінійний масштаб у вигляді мірної лінійки.
Це зручно, тому що за його наявності можна, скориставшись циркулем-вимірником або лінійкою, виміряти відстань на карті, прикласти його до лінійного масштабу й отримати результат, відповідний реальній відстані в заданих одиницях (найчастіше у км).
\(2\). Той масштаб, який пишеться у вигляді дробу, називається чисельним масштабом.
Такий масштаб показує, скільки одиниць вимірювання на місцевості відповідає одній такій самій одиниці вимірювання на карті (найчастіше у см). У даному прикладі \(1\)см на карті відповідають \(25\ 000\ 000\) см на місцевості, які зручніше перевести у км.
\(3\). Для того, аби не доводилося виконувати переведення чисельного масштабу, вказують іменований масштаб.
Він показує, яка саме відстань міститься в \(1\)см карти. У даному прикладі записано, що в \(1\)см міститься, відповідно, \(250\) км.
Приклад:
Користуючись картою масштабу \(1\) : \(12\ 500\ 000\), знайди відстань (по прямій лінії) між точками A і B на місцевості, якщо відстань на карті між ними дорівнює \(7\)см.
Розв'язання
На карті \(1\)см відповідає \(12\ 500\ 000\) см .Переведемо 12 500 000 см у км (12 500 000 см = 125 км).
Якщо в \(1\) см міститься \(125\) км, то в \(7\) см буде \(125\) · \(7\) \(=\) \(875\) км.
Відповідь: відстань між даними точками складає \(875\) км.
 |
Розв'язуючи завдання з масштабом:
|
Зверни увагу!
Більшим є той масштаб, за яким зроблено більш детальну карту. Чим більший масштаб , тим більше є зменшення. Але чим більше зменшення ,тим дрібнішими і менш виразними стають об'єкти на плані або на карті.
