Додати до числа \(a\) число \(b\) — означає змінити число \(a\) на \(b\) одиниць.
Будь-яке число від збільшення додатного числа збільшується, а від збільшення від'ємного числа зменшується.
Знайдемо суму чисел за допомогою координатної прямої.
Приклад:
Обчисли: \(3\) \(+\) \(2\) і \(3\) \(+\) \((-2)\)
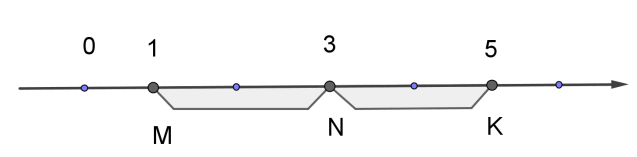
При переміщенні точки \(N\) \((3)\) на \(2\) одиниці праворуч, вона переходить у точку \(K\) \((5).\)
\(3\) \(+\) \(2\) \(=\) \(5\)
\(3\) \(+\) \(2\) \(=\) \(5\)
При переміщенні точки \(N\) \((3)\) на \(2\) одиниці ліворуч, вона переходить у точку \(M\) \((1).\)
\(3\) \(+\) \((-2)\) \(=\) \(1\)
\(3\) \(+\) \((-2)\) \(=\) \(1\)
Приклад:
Обчисли: \(-4\) \(+\) \(3\)
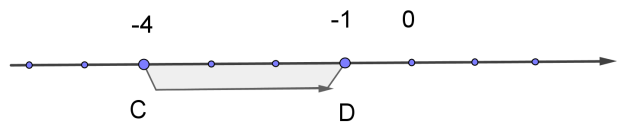
При переміщенні точки \(C\) \((-4)\) на \(3\) одиниці праворуч, вона переходить у точку \(D\) \((-1).\)
\(-4\) \(+\) \(3\) \(=\) \(-1\)
\(-4\) \(+\) \(3\) \(=\) \(-1\)
Приклад:
Обчисли: \(-3\) \(+\) \((-4)\)
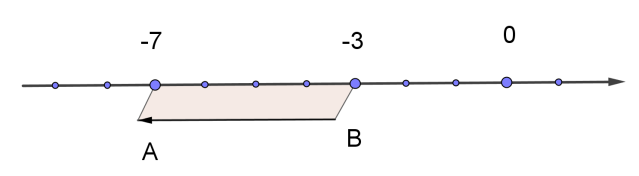
При переміщенні точки \(B\) \((-3)\) на \(4\) одиниці ліворуч, вона переходить у точку \(A\) \((-7).\)
\(-3\) \(+\) \((-4)\) \(=\) \(-7\)
\(-3\) \(+\) \((-4)\) \(=\) \(-7\)