За допомогою простого експерименту можна встановити:
яким би не було коло, відношення його довжини до діаметра є постійним числом.
Що потрібно для експерименту:
- гнучка рулетка для вимірювання;
- декілька круглих предметів (тарілки, вази).
Хід експерименту:
- необхідно виміряти довжину кола навколо предмета;
- хоча б приблизно виміряти діаметр кола;
- обчислити округлене ділення довжини кола на довжину діаметра кола (вибрати будь-яке число цифр за комою).
Звісно, результати будуть трохи відрізнятися (вимірювання дуже неточні), але буде помітно, що результатом завжди є число, близьке до \(3\).
Якщо провести більш точні вимірювання, можна знайти більш точне значення. Це число прийнято позначати буквою π (читається як «пі»).
Найчастіше використовують наближене значення числа π \(3,14\)
Більш точне значення:
π \(3,1415926535897932\)
Але цифр за комою набагато більше, і вони ніколи не повторюються. Завдяки розвитку обчислювальної техніки зовсім недавно стало можливим роздрукувати достатньо багато цифр числа π:

Ми маємо формулу для обчислення довжини кола, якщо відомий діаметр:
Якщо згадаємо, що , то формула довжини кола виглядатиме так:
Як же обчислити площу круга?
Один із підходів для визначення формули: уявімо, що круг перерізано наполовину, і кожну з половин поділено на рівні частини (на малюнку нижче):
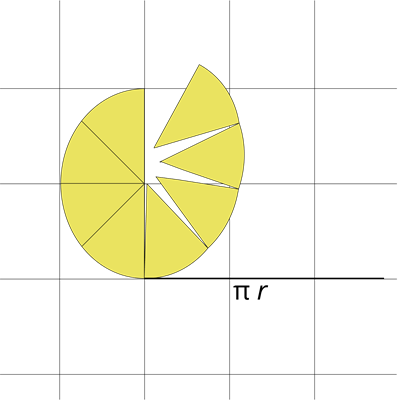
Із частин складемо прямокутник зі сторонами r і πr.

Для більш точного результату зменшимо частини круга, щоб складена фігура була якомога більше схожою на прямокутник.
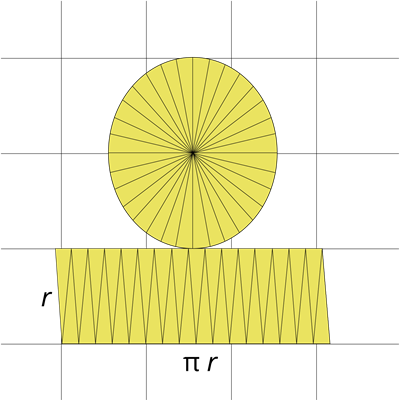
Ми бачимо, що площа круга обчислюється за формулою:
Сектор — це частина круга , обмежена дугою та двома радіусами, що з'єднують кінці дуги з центром круга.

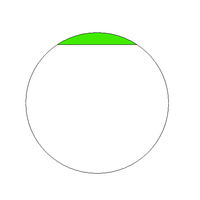
Сегмент — це частина круга ,обмежена дугою кола та її хордою.
Тіла обертання - циліндр , конус , куля.
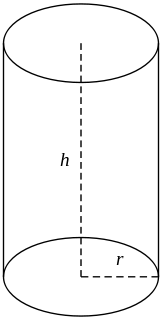
Циліндр — геометрична фігура , яка утворюється обертанням прямокутника навколо однієї зі своїх сторін.
Ця сторона зветься віссю циліндра.
Твірна циліндра — сторона прямокутника , що протилежна осі циліндра.
Циліндр має дві основи — круги радіуса r і бічну поверхню.
Площа бічної поверхні :
Площа повної поверхні циліндра :
Об'єм циліндра :
Слово циліндр походить від грецького слова kylindros, що означає "вал", "каток".
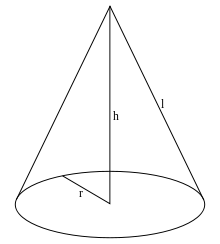
Конус — геометрична фігура , яка утворюється обертанням прямокутного трикутника навколо однієї із сторін, до яких прилягає прямий кут.
Ця сторона зветься віссю конуса. Вісь конуса є його висотою h.
Конус має одну основу — круг радіуса r і бічну поверхню.
Площа бічної поверхні конуса :
Площа повної поверхні конуса :
Об'єм конуса :
Конус походить від латинського слова "conus" , яке запозичене з грецької мови ("конос"- втулка , соснова шишка)
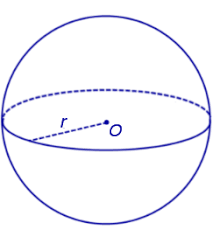
Куля — геометрична фігура , яка утворюється обертанням круга навколо його діаметру. Цей діаметр вважають віссю кулі.О- центр кулі, r — радіус кулі, D — діаметр кулі.
Площа поверхні кулі :
Об'єм кулі :
Слово "куля " походить від грецького слова "сфайра" — м'яч.