2. Методи розв'язування логарифмічних рівнянь

5.  Зведення до алгебраїчного.
 
Застосовують до рівнянь де може бути застосована підстановка, що зведе логарифмічне рівняння до алгебраїчного.
Приклад:
log3x+0.5=122log3x+1,    ОДЗ:x>13.Введемо підстановку 2log3x+1=t,⇒2log3x+1=t2.12⋅t2=12t,⇒t3=1,⇒t=13.t=1,⇒2log3x+1=1,⇒log3x=0,⇒x=1.Перевірка:log31+0.5=122log31+1,⇒0,5=0,5.Відповідь:x=1.
 
6.  Метод логарифмування.
  
Застосовують до рівнянь, якщо логарифм з невідомим знаходить в показнику степеня.
Приклад:
xlog3x+3=x2,      ОДЗ:x>0.log3x+3⋅log3x=2⋅log3x,log3x+3⋅log3x−2⋅log3x=0,log3x⋅log3x+1=0,log3x=0     або    log3x+1,x1=1,x2=13.Перевіркою встановлюємо, що обидва значення є коренями рівняння.Відповідь:x1=1,x2=13.
 
7.  Застосування властивостей логарифмів.
  
Метод застосовується до складних логарифмічних рівнянь, які можна звести до найпростішого логарифмічного рівняння, використавши властивості логарифмів.
 
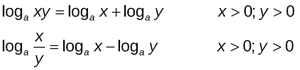
Рисунок19.png
 
8. Функціонально-графічний метод.
  
Використовують для аналізу кількості коренів рівняння монотонність функцій визначених рівнянням.
Приклад:
log520+x=7−x,                 ОДЗ:x>−20.Функція y=log520+x−зростає на всій області визначення, а функція y=4−x−спадає.Отже ці функції мають тільки одну точку перетину, тоді рівняння має один корін.Методом підбору можемо встановити, що x=5.Перевірка:log520+5=7−5,⇒2=2.Відповідь:x=5.
Більш докладно можна повторити дану тему у курсі алгебра 11 клас, тема "Логарифмічні рівняння".
Попередня теорія
Повернутись до теми
Наступне завдання
Copyright © 2025 МiйКлас