Показникові врази — урок. ЗНО/НМТ, Підготовка до ЗНО/НМТ з МійКлас.

Щоб легше було повторити матеріал згадаємо графік показникової функції.

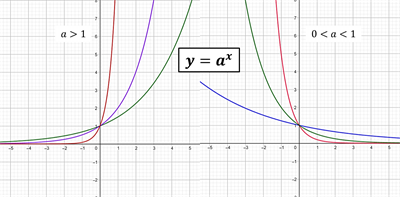
Показниковим називають вираз виду

a^{f (x)}

, де а — дійсне число.

У відповідності до означення можемо описати обмеження для \(а\), основи показникового виразу. Так, якщо \(а =1\), то отримуємо тотожність

1^{f (x)} = 1

(кажуть, що показникова функція вироджується в лінійну). Якщо а <0, то при певних значення а вираз

{(- a)}^{f (x)}

взагалі може не мати сенсу.

Для показникових виразів накладається умова:

\{\begin{cases} a > 0, \\ a \neq 1 . \end{cases}

Перетворення показникових виразів базується на властивостях степенів і арифметичних коренів. Розглянемо ці властивості.

Загальні властивості степеня.

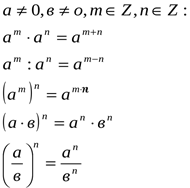
Властивості степеня з цілим показником.

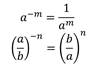
Властивості кореня.

Зверни увагу!

Якщо зустрічається складний вираз зі степенями, тобі складно і ти не розумієш як його розв'язати, то використовуй метод розкладання на множники. В результаті великі числа в основах степені замінюються більш простими і залишиться використати вище описані формули.

Приклад:

\begin{array}{l} \frac{128^{2 x + 1} \cdot 100^{5}}{625^{7} \cdot 2^{14 x - 1}} = \frac{{(2^{7})}^{2 x + 1} \cdot {(4 \cdot 25)}^{5}}{{(5^{4})}^{7} \cdot 2^{14 x - 1}} = \frac{2^{7 (2 x + 1)} \cdot {(2^{2} \cdot 5^{2})}^{5}}{5^{4 \cdot 7} \cdot 2^{14 x - 1}} = \frac{2^{14 x + 7} \cdot 2^{10} \cdot 5^{10}}{5^{28} \cdot 2^{14x - 1}} = \\ = 2^{14 x + 7 + 10 - 14 x + 1} \cdot 5^{10 - 28} = 2^{18} \cdot 5^{- 18} = {(\frac{2}{5})}^{18} = {0.4}^{18} . \end{array}

Попередня тема

Повернутись до теми

Наступна теорія

Відправити відгук

Знайшли помилку?

Розкажіть нам!

1. Показникові врази

Теорія: