Повторимо поняття синуса, косинуса і тангенса довільного кута.
Для описання довільного кута використовують одиничне коло: коло радіуса одиниця, з центром в початку відліку і початковим положення положенням радіус-вектора ОВ.
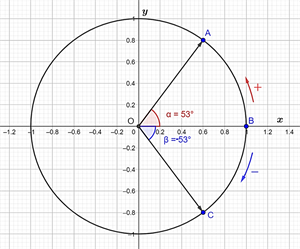
Обертаємо радіус вектор навколо початку відліку і отримаємо положення ОА.
При повороті початкового радіуса проти руху годинникової стрілки кут повороту вважають додатним, а за рухом годинникової стрілки — від'ємним.
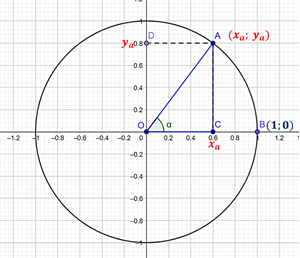
Синусом кута називають ординату точка А
Косинусом кута називають абсциссу точки А.
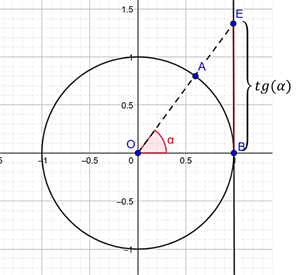
Тангенсом кута називають відношення ординати кінця одиничного рухомого радіуса до його абсциси:
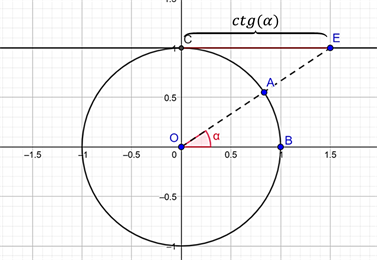
Котангенсом кута називають відношення абсциси кінця одиничного рухомого радіуса до його ординати:
Зверни увагу!
Пряму ВЕ — пряма тангенсів, а пряма СЕ — пряма котангенсів.
Для довільного кута
У залежності від координатної чверті тригонометричні функції змінюють свій знак, як показано на рисунку нижче.
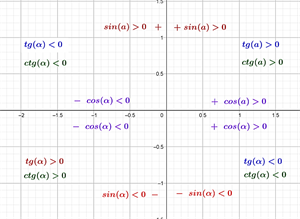
Функції — не парні, а функція — парна.
Відповідно справедливі наступні тотожності:.
Усі тригонометричні функції періодичні. Найменші додатні періоди функцій i . На періодичності тригонометричних функцій визначаються формули зведення.
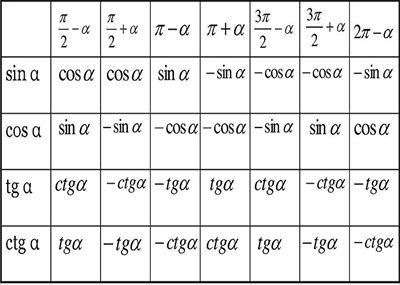
Більш докладно повторити матеріал можна в курсі геометрії 8 клас, в курсі алгебри 10 клас.
