Щоб легше було повторити матеріал згадаємо графік логарифмічної функції.
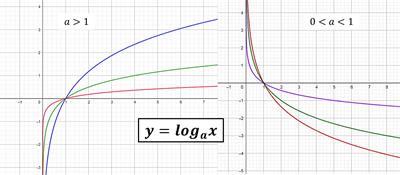
Логарифмом числа \(b > 0\) за основою \(a > 0\), \(a ≠ 1\), називається показник степеня, до якого треба піднести число a, щоб отримати число \(b\).
Математика вивчає логарифми з будь-якими позитивними основами. Однак на практиці найбільш поширені три їх види:
— десятковий логарифм, основа якого дорівнює \(10\), ;
— двійковий логарифм, основа якого дорівнює \(2\), ;
— найважливішим є натуральний логарифм, . Це логарифм, основою якого є число e, приблизно рівне \(2,71828\).
Логарифмічним називається математичний вираз виду або , де \(a\) — дійсне число.
Зверни увагу!
У відповідності до означення можемо описати обмеження для значення \(a\). Для виразу маємо: . Вираз має зміст при \(a > 0\).
Розглянемо основні формули, які треба знати, щоб впоратися з логарифмами.
Наслідки означення.

Властивості математичних дій.
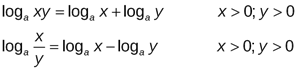
Властивості степенів основи і підлогарифмічного виразу.
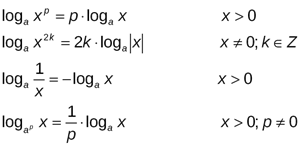
Формули переходу до нової основи.
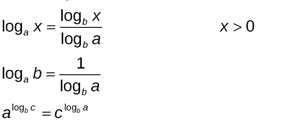
Більш докладно повторити тему «Логарифмічні вирази» можна повторити в курсі алгебра 11 клас.