Теорія — урок. ЗНО з математики, Алгебра.

Рівняння називають показниковим, якщо невідома міститься у показнику степеня.

a^{f (x)} = b; a^{f (x)} = b^{f (x)}; a^{f (x)} = a^{f (x)} .

Методи розв'язування показникових рівнянь.

Метод логарифмування.

Рівняння зводиться до найпростішого і логарифмують обидві частини рівняння.

Приклад:

8^{x} = 15, \Rightarrow \log_{8} 8^{x} = \log_{8} 15, \Rightarrow x \cdot \log_{8} 8 = \log_{8} 15, \Rightarrow x = \log_{8} 15 .

За означенням степеня.

Використовується, якщо в обох частинах степеневі вирази мають однакову основу.

Приклад:

24^{x^{2}} = 24^{9}, \Rightarrow x^{2} = 9, \Rightarrow x = \pm 3 .

Зведення до однієї основи.

Розглянемо на прикладі.

Приклад:

15^{4 x + 7} = 1, \Rightarrow 15^{4 x + 7} = 15^{0}, \Rightarrow 4 x + 7 = 0, \Rightarrow 4 x = - 7, \Rightarrow x = - 1 \frac{3}{4} .

Метод підстановки.

Степеневий вираз замінюємо на нову змінну, спрощуючи основне рівняння.

\begin{array}{l} 9^{2x - 1} - 3^{2x - 1} = 0, \Rightarrow 3^{2 (2 x - 1)} - 3^{2x - 1} = 0 . \\ 3^{2x - 1} = t, 3^{2 (2x - 1)} = t^{2} . \\ t^{2} - t = 0, \Rightarrow t (t - 1) = 0, \Rightarrow t_{1} = 0, t_{2} = 1 . \\ t_{1} = 0 \Rightarrow 3^{2x - 1} = 0, \Rightarrow x \in \emptyset . \\ t_{2} = 1 \Rightarrow 3^{2x - 1} = 1, \Rightarrow 3^{2x - 1} = 3^{0}, \Rightarrow 2 x - 1 = 0, \Rightarrow x = 0.5 . \end{array}

Однорідні показникові рівняння.

Рівняння виду

a^{f (x)} = b^{f (x)}

називається однорідним.

Зверни увагу!

Так, як показникова функція не може приймати значення "0", то обидві частини рівняння можна поділити на

b^{f (x)}

\begin{array}{l} 1 . 21 \cdot 7^{x + 1} = 3^{x + 1} \cdot 49, \Rightarrow \frac{7^{x + 1}}{3^{x + 1}} = \frac{49}{21}, \Rightarrow {(\frac{7}{3})}^{x + 1} = {(\frac{7}{3})}^{2}, \Rightarrow \\ \Rightarrow x + 1 = 2, \Rightarrow x = 1 . \end{array}

\begin{array}{l} 2 . 9^{x} + 3 \cdot 2^{x} \cdot 3^{x} - 10 \cdot 4^{x} = 0, \\ 3^{2 x} + 3 \cdot 2^{x} \cdot 3^{x} - 10 \cdot 2^{2 x} = 0, \\ \frac{3^{2 x}}{2^{2 x}} + 3 \cdot \frac{3^{x}}{2^{x}} - 10 = 0, \\ {(\frac{3}{2})}^{2 x} + 3 \cdot {(\frac{3}{2})}^{x} - 10 = 0, \\ t^{2} + 3t - 10 = 0, \\ t_{1} = - 5, t_{2} = 2 . \\ t_{1} = - 5, \Rightarrow {(\frac{3}{2})}^{x} = - 5, x \in \emptyset . \\ t_{2} = 2, \Rightarrow {(\frac{3}{2})}^{x} = 2, \Rightarrow \log_{1.5} {(1.5)}^{x} = \log_{1.5} 2, \Rightarrow x = \log_{1.5} 2 . \end{array}

Метод розкладання на множники.

Приклад:

3^{x + 2} - 7 \cdot 3^{x} = 2, \Rightarrow 3^{x} \cdot (3^{2} - 7) = 2, \Rightarrow 3^{x} \cdot 2 = 2, \Rightarrow 3^{x} = 1, \Rightarrow x = 0 .

Функціонально-графічний метод.

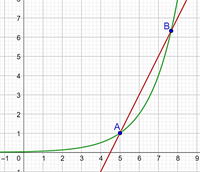
\begin{array}{l} 2^{x - 5} = 2 x - 9, \{\begin{cases} y = 2^{x - 5}, \\ y = 2 x - 9 . \end{cases} \\ Побудуємо описані графіки (рис . 1) і знайдемо точки перетину : т . А (5; 1), \\ т . В (7,7; 6,3) . Абсциси точок перетину і будуть коренями рівння . \\ Відповідь : x_{1} = 5, x_{2} = 7.7 . \end{array}

рис. 1

Знайшли помилку?

1. Теорія