Функція кубічного кореня — урок. Алгебра, 10 клас.

Функція

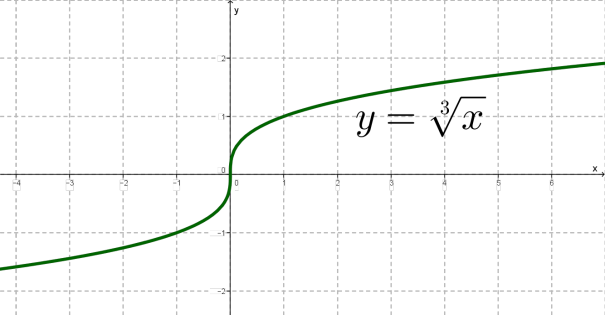
y = \sqrt[3]{x}

\(,\) її властивості і графік

Число \(b\) називають кубічним коренем (або коренем третього степеня) з числа \(a,\) якщо виконується рівність

b^{3} = a

\(.\)

Пишуть:

\sqrt[3]{a} = b

\(,\) де \(a\) — підкореневе число, \(3\) — показник кореня.

Отже, рівності

\sqrt[3]{a} = b

\(,\)

b^{3} = a

\(,\)

{(\sqrt[3]{a})}^{3} = a

— еквівалентні, тобто виражають одну й ту саму залежність між дійсними числами \(a\) і \(b.\)

Коротше це можна записати так:

\sqrt[3]{a} = b \Leftrightarrow b^{3} = a

\(;\)

\Leftrightarrow

— знак еквівалентності.

Наприклад:

\begin{array}{l} \sqrt[3]{27} = 3, бо 3^{3} = 27 \\ \sqrt[3]{1} = 1, бо 1^{3} = 1 \\ \sqrt[3]{0} = 0, бо 0^{3} = 0 \end{array}

Зверни увагу!

Кубічний корінь

\sqrt[3]{a}

існує для будь-якого числа \(a.\)

Результат добування кубічного кореня порівняно рідко виявляється раціональним числом.

Найчастіше виходить ірраціональне число, для якого можна знайти тільки наближене значення.

Властивості функції

y = \sqrt[3]{x}

\(1.\)

D (f) = (- \infty; + \infty)

\(.\)

\(2.\) Непарна.

\(3.\) Зростає на числовій прямій.

\(4.\) Необмежена ні знизу, ні зверху.

\(5.\) Не має ні найменшого, ні найбільшого значень.

\(6.\) Неперервна на всій числовій прямій.

\(7.\)

E (f) = (- \infty; + \infty)

\(.\)

\(8.\) Опукла вниз на

(- \infty; 0]

та опукла вгору на

[0; + \infty)

\(.\)

Знайшли помилку?

1. Функція кубічного кореня