1. Обернена функція

Функція, яка приймає кожне своє значення в єдиній точці області визначення, є оборотною. Це означає, якщо функція y=f(x) є оборотною й існує число а, що належить до її області значень E(f), то рівняння f(x)=a має розв’язок, причому єдиний.
У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає. Функції y=x,y=1x,y=x є прикладами оборотних функцій.
Функцію \(y=f(x),\) x∈X називають оберненою, якщо вона набуває будь-якого свого значення тільки в одній точці множини \(X\) (інакше кажучи, якщо різним значенням аргументу відповідають різні значення функції).
Теорема \(1\)
 
Якщо функція \(y=f(x),\) x∈X монотонна на множині \(X,\) то вона обернена. 
 
Нехай \(y=f(x),\) x∈X — обернена функція та E(f)=Y\(.\) Поставимо у відповідність кожному \(y\) з \(Y\) єдине значення \(x,\) за якого f(x)=y (тобто єдиний корінь рівняння f(x)=y відносно змінної \(x\)). Тоді отримаємо функцію, яка визначена на \(Y,\) а \(X\) — область її значень. Цю функцію позначають x=f−1(y),y∈Y і називають оберненою по відношенню до функції \(y=f(x),\) x∈X\(.\)
Теорема \(2\)
 
Якщо функція \(y=f(x)\) зростає (спадає) на множині \(X,\) а \(Y\) — область значень функції, то обернена функція x=f−1(y),y∈Y зростає (спадає) на множині \(Y.\)
Теорема \(3\)
 
Точки \(M\) \((a; b)\) і \(P\) \((b; a)\) симетричні відносно прямої \(y=x.\) (Графіки прямої і оберненої функції симетричні відносно прямої \(y=x.\))
Знаходження формули для функції, що обернена даній
Користуючись формулою \(y = f(x),\) слід виразити \(x\) через \(y,\) а в отриманій формулі \(x = g(y)\) замінити \(x\) на \(y,\) а \(y\) — на \(x.\)
Приклад:
Дано функцію y=x2,x∈0;+∞)\(.\) Знайди обернену функцію.

Розв'язання
 
Задана функція зростає на проміжку 0;+∞)\(,\) отже, вона має обернену функцію. Із рівняння y=x2 знаходимо: x=y або x=−y\(.\)

Проміжку 0;+∞) належать лише значення функції x=y\(.\) Це і є обернена функція, яка визначена на проміжку 0;+∞)\(.\)
 
Помінявши місцями \(x\) і \(y,\) отримаємо: y=x,x∈0;+∞)\(.\) Графік цієї функції виходить із графіка функції y=x2,x∈0;+∞) за допомогою симетрії відносно прямої \(y=x.\)
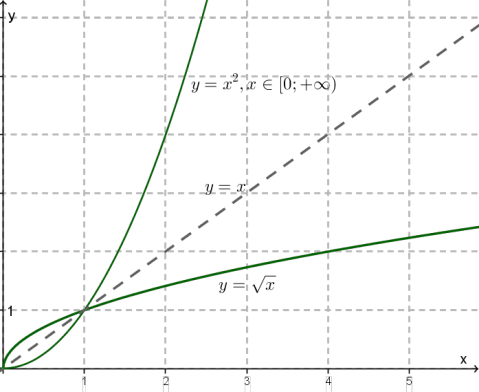
obratnaja.png
Зверни увагу!
Функція y=x2 не є оборотною. Проте, y=x2,x∈0;+∞) є оборотною. Кажуть, що функція y=x2 є оборотною на множині 0;+∞). 
Джерела:
Алгебра і початки аналізу: профільний рівень: підручник для 10 кл. А.Г. Мерзляк. та ін.- Х.:Гімназія,2018.
Попередня тема
Повернутись до теми
Наступне завдання
Copyright © 2025 «МійКлас»