Функцію \(y=f(x),\) називають парною, якщо для будь-якого значення \(x\) із множини \(X\) виконується рівність \(.\)
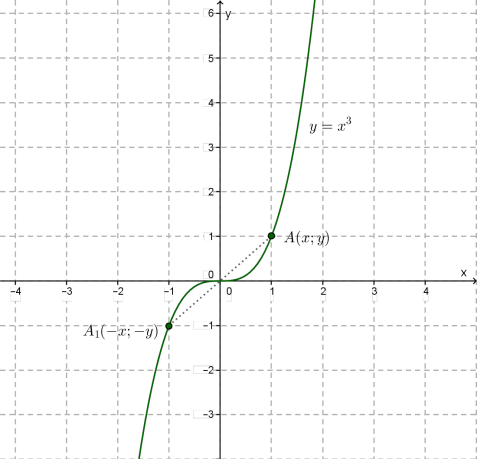
Функцію \(y=f(x),\) називають непарною, якщо для будь-якого значення \(x\) із множини \(X\) виконується рівність \(.\)
Функція може бути парною, непарною, а також ні парною, ні непарною.
Вивчення питання про те, чи є задана функція парною або непарною, називається дослідженням функції на парність.
Якщо функція \(y=f(x)\) — парна або непарна, то її область визначення \(D(f)\) — симетрична множина.
Алгоритм дослідження функції \(y = f (x)\) на парність
\(2.\) Скласти вираз \(f(-x).\)
\(3.\) Порівняти \(f(-x)\) та \(f(x)\)\(:\)
\(a)\) якщо для будь-якого \(,\) то функція парна;
\(b)\) якщо для будь-якого \(,\) то функція непарна;
\(a)\) якщо для будь-якого \(,\) то функція парна;
\(b)\) якщо для будь-якого \(,\) то функція непарна;
\(c)\) якщо хоча б в одній точці виконується співвідношення і хоча б в одній точці виконується співвідношення \(,\) то функція \(y=f(x)\) не є ні парною, ні непарною.
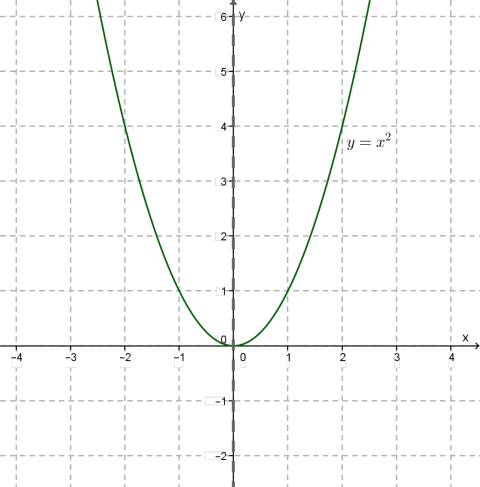
Якщо графік функції \(y = f (x)\) симетричний відносно осі ординат, то \(y = f (x)\) — парна функція.
Якщо графік функції \(y = f (x)\) симетричний відносно початку координат, то \(y = f (x)\) — непарна функція.