У функції вигляду — натуральне число, яке називається степеневою функцією з від'ємним цілим показником.
Тому замість запису можна використовувати запис \(.\)
Функція
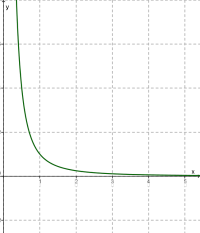
Властивості функції
\(1)\) \(;\)
\(2)\) спадна;
\(3)\) обмежена знизу, необмежена зверху;
\(4)\) не має ні найбільшого, ні найменшого значень.
\(3)\) обмежена знизу, необмежена зверху;
\(4)\) не має ні найбільшого, ні найменшого значень.
Функція
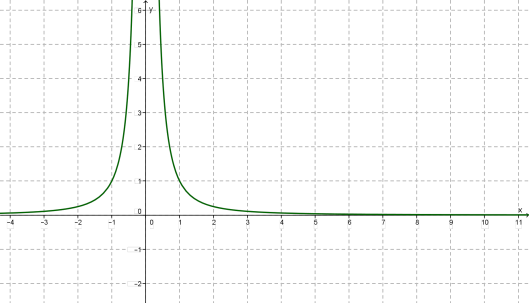
Властивості функції
\(1)\) \(;\)
\(2)\) парна;
\(3)\) спадає на відкритому промені \(,\) зростає на відкритому промені \(;\)
\(3)\) спадає на відкритому промені \(,\) зростає на відкритому промені \(;\)
\(4\) обмежена знизу, необмежена зверху;
\(5)\) не має ні найбільшого, ні найменшого значень;
\(6)\) неперервна при \(x <0\) (тобто відкритому промені та при \(x>0\) (тобто відкритому промені \(;\)
\(5)\) не має ні найбільшого, ні найменшого значень;
\(6)\) неперервна при \(x <0\) (тобто відкритому промені та при \(x>0\) (тобто відкритому промені \(;\)
\(7)\) \(;\)
\(8)\) опукла вниз і при \(x<0,\) і при \(x>0.\)
Функція
Зазначимо, що крива асимптотично наближається до осей координат. Кажуть також, що вісь \(x\) є горизонтальною асимптотою графіка функції \(,\) а вісь \(y\) — вертикальною асимптотою цього графіка.
Функція
Зазначимо, що вісь \(x\) є горизонтальною асимптотою графіка функції \(,\) а вісь \(y\) — вертикальною асимптотою цього графіка.
Властивості функції
\(1)\) \(;\)
\(2)\) непарна;
\(3)\) спадає на відкритому промені та на відкритому промені \(;\)
\(3)\) спадає на відкритому промені та на відкритому промені \(;\)
\(4\) необмежена ні знизу, ні зверху;
\(5)\) не має ні найбільшого, ні найменшого значень;
\(6)\) неперервна при \(x <0\) і при \(x>0\)\(;\)
\(5)\) не має ні найбільшого, ні найменшого значень;
\(6)\) неперервна при \(x <0\) і при \(x>0\)\(;\)
\(7)\) \(;\)
\(8)\) опукла вгору при \(x<0,\) опукла вниз при \(x>0.\)