1. Рівняння дотичної до графіка функції

Нехай дана функція \(y=f(x)\) і точка \(M(a; f(a))\); нехай відомо, що існує $f^{\prime }(a)$. 
Утворимо рівняння дотичної до графіка заданої функції в заданій точці.
Це рівняння, як рівняння будь-якої прямої, не паралельної осі ординат, має вигляд \(y=kx+m\), тому завдання полягає в знаходженні значень коефіцієнтів \(k\) і \(m\).

Відомо, що $k=f^{\prime }(a)$. Для обчислення значення \(m\) скористаємося тим, що шукана пряма проходить через точку \(M(a; f(a))\).
Це означає, що якщо підставити координати точки \(M\) в рівняння прямої, отримаємо правильну рівність \(f(a)=ka+m\), тобто \(m=f(a)-ka\).

Залишилося підставити знайдені значення коефіцієнтів \(k\) і \(m\) в рівняння прямої:

$\begin{array}{l}y=\mathit{kx}+m\\ y=\mathit{kx}+(f(a)-\mathit{ka})\\ y=f(a)+k(x-a)\\ \\ y=f(a)+f^{\prime }(a)(x-a).\end{array}$

Нами отримано рівняння дотичної до графіка функції \(y=f(x)\) в точці \(x=a\).

Для функції \(y=f(x)\), що має похідну у фіксованій точці \(x\), справедлива наближена рівність $\mathrm{\Delta }y\approx f^{\prime }(x)\cdot \mathrm{\Delta }x$

або, докладніше, $f(x+\mathrm{\Delta }x)-f(x)\approx f^{\prime }(x)\cdot \mathrm{\Delta }x$.

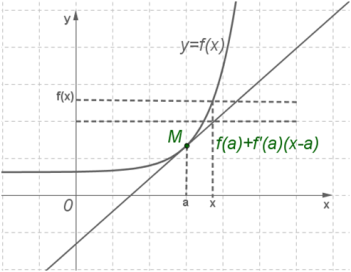
Для зручності подальших міркувань змінимо позначення: замість \(x\) будемо писати \(a\), замість $x+\mathrm{\Delta }x$ будемо писати \(x\) і, відповідно, замість $\mathrm{\Delta }x$ будемо писати \(x-a\). Тоді написана вище наближена рівність набуде вигляду:

$\begin{array}{l}f(x)-f(a)\approx f^{\prime }(a)(x-a)\text{ або}\\ f(x)\approx f(a)+f^{\prime }(a)(x-a)\end{array}$

Cмисл наближеної рівності в тому, що в якості наближеного значення функції в точці \(x\) беруть значення ординати дотичної в тій же точці.