Точки і отримані поворотом точки \((1;0)\) на кути і відповідно.
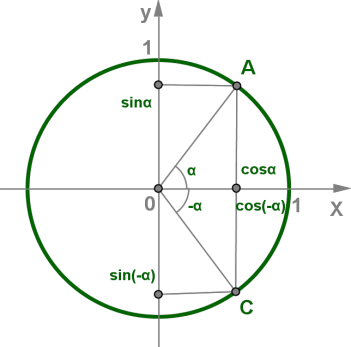
Одиничне коло.
Абсциси цих точок співпадають, а ординати відрізняються тільки знаками, тобто .
Отже, функція є непарною функцією, а - парною функцією. Функція , тому буде правильна рівність , тобто функція — непарна функція.
Функція називається періодичною, якщо існує таке число , що для будь-якого з області визначення цієї функції виконується рівність .
Число називається періодом функції .
З цього визначення випливає, що якщо належить області визначення функції , то числа також належать області визначення цієї періодичної функції і .
Повернув точку навколо центру одиничного кола в додатному або від'ємному напрямі, помічаємо що вона повернеться до вихідного положення, тільки кут повороту буде на більше або менше, але координати точки залишаться тими ж, тобто
Отже, число є найменшим додатним періодом для функцій і .
Число є найменшим додатним періодом для функцій , тому що значення тангенса кута повороту буде повторюватися через радіан.
