Тригонометричні функції кутового аргументу.
Із термінами "синус", "косинус", "тангенс", "котангенс" ми зустрічалися і раніше в геометрії, коли розглядали синус, косинус, тангенс і котангенс кута, а не числа, як було в попередніх темах.
Насправді, ці два підходи до даних визначень тісно пов'язані між собою.
Візьмемо кут із градусною мірою і розташуємо його в числовому колі на координатній площині так, щоб вершина кута сполучилася з центром кола (початком системи координат), одна сторона кута сполучилася з додатним променем осі абсцис, а друга сторона перетинала б коло у точці \(M\) (див. мал.).
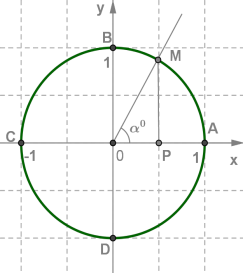
Ордината точки \(M\) називається синусом кута , а абсциса точки \(M\) називається косинусом кута .
Кожен раз виконувати такі побудови необов'язково, достатньо зауважити, що дуга \(AM\) становить таку ж частину одиничного кола, яку кут складає від кута .
Позначив довжину дуги \(AM\) буквою \(t\), отримаємо рівність:
Кажуть, що - це градусна міра кута, а - це радіанна міра того ж кута.
Тобто \(=\) рад.
Отже,
рад. або
\(1\) рад \(=\)
Приклад:
рад;
рад \(=\)
Позначення рад зазвичай не пишуть, тобто цілком допустимий запис
\(=\) .
Кут в - це центральний кут, що спирається на дугу, яка становить частину кола.
Кут в \(1\) радіан - це центральний кут, що спирається в одиничному колі на дугу довжиною \(1\).
Із формули
\(1\) рад \(=\) отримуємо, що \(1\) рад
Розглянув ту чи іншу тригонометричну функцію, можна вважати її функцією як числового, так і кутового аргументу.
Приклад:
