Арккосинус і рівняння cos x = a — урок. Алгебра, 10 клас.

Тригонометричне рівняння — рівняння, що містить невідоме під знаком тригонометричної функції.

Рівняння виду

\sin x = a, \cos x = a, tg x = a, ctg x = a

називаються найпростішими тригонометричними рівняннями.

Рівняння

\cos x = a

Якщо

|a| > 1

, тоді рівняння

\cos x = a

не має коренів.

Наприклад, рівняння

\cos x = - 1,5

не має коренів.

Якщо

|a| \leq 1

, тоді корені рівняння виражаються формулою

x = \pm \arccos a + 2 π k, k \in ℤ

Що ж таке

\arccos a

? Арккосинус в перекладі з латинської означає дуга і косинус. Це зворотна функція.

Якщо

|a| \leq 1

, тоді

\arccos a

(арккосинус

а

) - це таке число з відрізка

[0; π]

, косинус якого дорівнює

а

Говорячи інакше:

\arccos a = x \Rightarrow \cos x = a, |a| \leq 1, x \in [0; π]

Приклад:

Знайти

\arccos \frac{\sqrt{2}}{2}

Вираз

\arccos \frac{\sqrt{2}}{2}

показує, що косинус кута

x

дорівнює

\frac{\sqrt{2}}{2}

(

\cos x = \frac{\sqrt{2}}{2}

Далі просто знаходимо точку цього косинуса на числовому колі, що і є відповіддю:

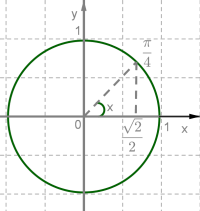
число, що є значенням осі

x

, відповідає точці

\frac{π}{4}

на числовому колі.

Отже,

\arccos \frac{\sqrt{2}}{2} = \frac{π}{4}

Зверни увагу!

якщо

\cos \frac{π}{4} = \frac{\sqrt{2}}{2}

, тоді

\arccos \frac{\sqrt{2}}{2} = \frac{π}{4}

У першому випадку по точці на числовому колі визначаємо значення косинуса, а в другому - навпаки, за значенням косинуса знаходимо точку на числовому колі. Рух у зворотний бік. Це і є арккосинус.

Теорема. Для будь-якого