Якщо дано числову множину \(X\) і правило \(f,\) що дозволяє поставити у відповідність кожному елементу \(x\) із множини \(X\) певне число \(y,\) то кажуть, що задано функцію \(y = f (x)\) із областю визначення \(X.\)
Областю визначення функції \(y = f(x)\) називається множина всіх значень \(x,\) для яких функція має зміст.
Множина всіх значень функції \(y = f(x),\) називається областю значень функції.
Зверни увагу!
Пишуть:
\(x\) — незалежна змінна (аргумент);
\(y\) — залежна змінна;
\(D(f)\) — область визначення функції;
\(E(f)\) — область значення функції.
Задати функцію — означає вказати правило, яке дозволяє за довільно вибраним значенням обчислити відповідні значення \(y.\)
Способи задання функції
\(1.\) Графічний: функція задається графікомЯкщо дано функцію і на координатній площині \(xOy\) позначені всі точки вигляду \((x; y),\) де \(,\) а \(,\) то множину цих точок називають графіком функції \(.\)
Приклад:
\(y=kx+m\) — пряма
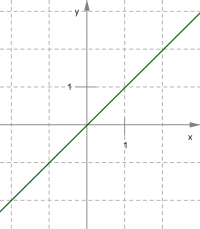
\(2.\) Аналітичний: функція задається формулою
Приклад:
Приклад:
\(x\) | \(1\) | \(2\) | \(3\) | \(4\) |
\(y\) | \(1\) | \(4\) | \(9\) | \(16\) |
\(4.\) Числові пари
Приклад: