Число називають границею послідовності , якщо в будь-якому, заздалегідь обраному околі точки , містяться всі члени послідовності, починаючи з деякого номера.
або .
Пояснення до даного визначення:
околом точки радіуса є інтервал , .
Візьмемо інтервал , тобто, окіл точки ; — радіус цього околу . Існує номер починаючи з якого, вся послідовність міститься у зазначеному околі: і т.д.
Приклад:
Дана послідовність :
Довести, що
Розв'язок.
Візьмемо будь-який окіл точки , нехай її радіус дорівнює .
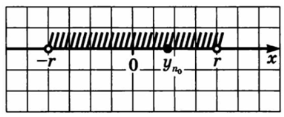
Завжди можна підібрати натуральне число , так щоб виконувалася нерівність .
Якщо, , тоді в якості можна взяти , оскільки , і т.д.
Це означає, що член послідовності з номером , тобто , потрапляє в обраний окіл точки . Тим більше в цьому околі будуть знаходитися всі наступні члени заданої спадної послідовності . Відповідно до визначення це і означає, що .
Для наочності побудуємо графік послідовності , який утворений із точок з абсцисами , які лежать на гілці гіперболи .
Оскільки , тоді пряма є горизонтальною асимптотой графіка функції .