Кажуть, що функція \(y=f(x)\), має період \(T\), якщо для будь-якого виконуються рівності .
Функцію, що має відмінний від нуля період \(T\), називають періодичною.
Якщо функція \(y=f(x)\), має період \(T\), тоді будь-яке число, кратне \(T\), також є її періодом.
Найменшим додатнім періодом функції називається найменше з додатних чисел \(T\), які є періодом даної функції.
Прикладом періодичних функцій можуть служити тригонометричні функції \(y = sin\) \(x\), \(y = cos\) \(x\) (період цих функцій дорівнює ), \(y = tg\) \(x\) (період дорівнює ) та інші. Функція \(y = cons\) \(t\) також є періодичною. Для неї періодом є будь-яке число
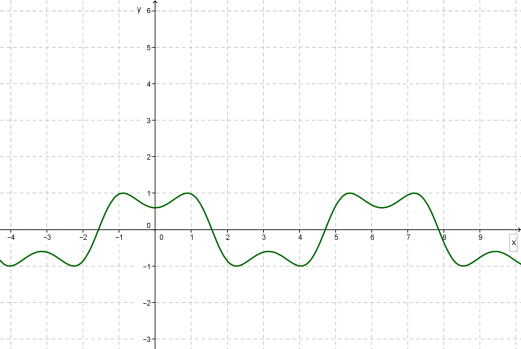
Графік періодичної функції будують на проміжку , а потім повторюють на всю область визначення.
Побудуємо графік функції