Синус і косинус гострого кута прямокутного трикутника визначається так:
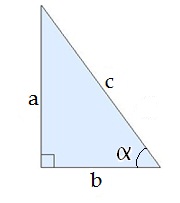 |
Яке відношення одиничне коло має до цих тригонометричних функцій?
Одиничне коло можна використовувати, як інструмент для зчитування значень тригонометричних функцій.
Значення синуса кута повороту читаються з осі \(Oy\). 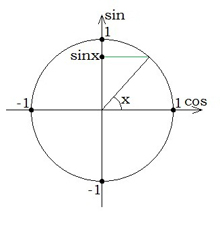 | Значення косинуса кута повороту читаються з осі \(Ox\). 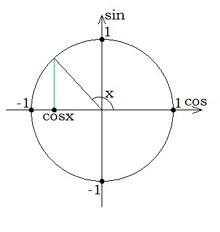 |
Найчастіше одиничне коло використовується для визначення знака тригонометричної функції, числові значення знаходяться в таблицях або обчислюються за допомогою калькулятора.
Знаки синуса в квадрантах 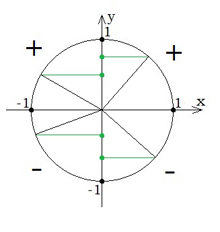 | Знаки косинуса в квадрантах 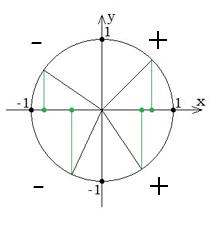 |
Важливо вміти зчитувати з кола наступні значення синуса і косинуса:
\(sin\) \(0^{\circ}=0\) \(sin\) \(90 ^{\circ}=1\) \(sin\) \(180^{\circ}=0\) \(sin\) \(270 ^{\circ}=-1\) \(sin\) \(360^{\circ}=0\) 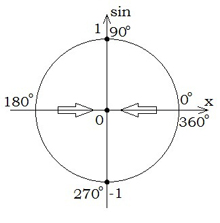 | \(cos\) \(0^{\circ}=1\) \(cos\) \(90 ^{\circ}=0\) \(cos\) \(180^{\circ}=-1\) \(cos\) \(270 ^{\circ}=0\) \(cos\) \(360^{\circ}=1\) 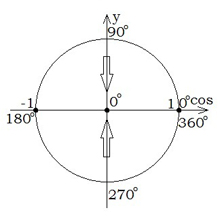 |
Значення тригонометричних функцій, які потрібно знати напам'ять.
| \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | |
| \(sin\) | |||
| \(cos\) | |||
| \(tg\) | \(1\) |