У комбінаториці розглядаються два істотно різні види комбінацій.
Комбінації, в яких має значення порядок елементів, називаються розміщеннями.
У розміщеннях у кожного елементу своя певна роль. Наприклад, пара учнів — староста класу та його помічник, пара цифр — десятки й одиниці.
Зверни увагу!
Розміщення — це впорядковані набори.
Комбінації, при складанні яких важливо знати тільки те, які елементи вибрані, але їх порядок не має значення, називаються комбінаціями.
Зверни увагу!
Комбінації не є впорядкованими наборами.
В обох видах кількість комбінацій можна знайти за допомогою деревоподібної діаграми.
Приклад:
Скількома різними способами можна вибрати пару чергових, якщо в класі залишилися \(4\) учні: Надя, Віка, Саша та Юра?
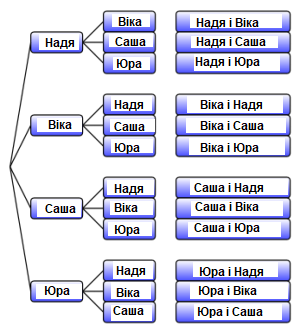
На діаграмі видно, що можна скласти \(6\) пар чергових: Надя і Віка, Надя і Юра, Надя і Саша, Віка і Саша, Саша і Юра, Віка і Юра, оскільки кожна пара повторюється по \(2\) рази.
У цьому прикладі було знайдено кількість комбінацій.
Використовуючи цю ж деревоподібну діаграму, розв'яжемо іншу задачу:
Скількома різними способами можна вибрати двох учнів (одного витирати дошку, іншого підмітати підлогу), якщо в класі залишилися Надя, Віка, Саша і Юра?
Скількома різними способами можна вибрати двох учнів (одного витирати дошку, іншого підмітати підлогу), якщо в класі залишилися Надя, Віка, Саша і Юра?
У такому випадку відповідь буде \(12\) пар, оскільки кожен учень виконує своє завдання.
Якщо їх поміняти місцями, вони поміняють і свої функції.
У цьому прикладі було знайдено кількість розміщень.
Якщо їх поміняти місцями, вони поміняють і свої функції.
У цьому прикладі було знайдено кількість розміщень.
За допомогою деревоподібної діаграми можна отримати й кількість комбінацій, і кількість розміщень, але її зручно використовувати тільки тоді, коли кількість елементів невелика.
