Різниця найбільшого і найменшого значень випадкової величини вибірки називається її розмахом і позначається \(R.\)
Приклад:
Задано вибірку \(80, 80, 330, 4500.\) Розмах: \(R=4500-80=4420.\)
Відхиленням від середнього називається різниця між розглянутим значенням випадкової величини і середнім значенням вибірки.
Приклад:
Задано вибірку \(52, 54, 50, 48, 46.\)
Нехай значення величини \(,\) а значення середнього \(,\) відхилення від середнього \(.\)
Середнє арифметичне квадратів відхилень називається дисперсією і позначається \(D.\)
Для оцінки степеня відхилення від середнього значення зручно мати справу з величиною тієї самої вимірності, що й сама величина \(X.\) Із цією метою використовують значення квадратного кореня з дисперсії \(.\)
Квадратний корінь із дисперсії називають середнім квадратичним відхиленням і позначають .
Кореляція, кореляційна залежність — статистичний взаємозв'язок двох або декількох випадкових величин. При цьому зміни значень однієї або декількох із цих величин супроводжують систематичну зміну значень іншої або інших величин.
На координатній площині кожному досліджуваному елементу відповідає точка, абсциса (\(x\)) якої є числовим значенням однієї ознаки цього елемента, а ордината (\(y\)) — відповідним числовим значенням іншої ознаки цього елемента.
Якщо таким чином додати значення двох ознак, і точки будуть розташовані приблизно на прямій, яка відповідає спадній або зростаючій функції, то між ознаками існує кореляція.
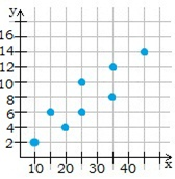
Додатна кореляція (точки розташовані приблизно на прямій, що відповідає зростаючій функції) існує, коли при збільшенні значення однієї ознаки збільшуються значення іншої ознаки.
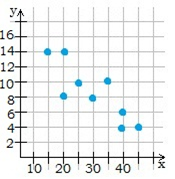
Від'ємна кореляція (точки розташовані приблизно на прямій, що відповідає спадній функції) існує, коли при збільшенні значення однієї ознаки зменшується значення іншої ознаки.
Якщо між ознаками кореляції не існує, то зміна значення однієї ознаки не впливає на зміну іншої ознаки.