Статистика займається збором, зображенням (у вигляді таблиць, діаграм, графіків та ін.) та аналізом інформації про різні випадкові величини.
Випадковими величинами (даними) називаються такі величини, які в ході спостережень або випробувань можуть приймати різні значення. Можна говорити про те, що їхні значення залежать від випадку.
Значення змінних, які реєструються за допомогою чисел, що мають змістовне значення, називаються кількісними даними.
Залежно від того, які значення може потенційно приймати змінна, виокремлюють два типи кількісних даних:
\(1)\) дискретні;
\(2)\) неперервні.
Якщо два варіанти ознаки в даній сукупності можуть відрізнятися один від одного не менш ніж на певне число або взагалі збігаються, то такі дані називаються дискретними.
Наприклад, кількість учнів у класах школи; кількість балів, які набирає учень під час тестування; кількість дітей у сім'ї; кількість викликів швидкої допомоги, що надходять до лікарні; кількість клієнтів, що звернулися до фірми за певний проміжок часу і т. п.
Якщо випадкова величина може приймати будь-яке значення з деякого проміжку, то така величина називається неперервною.
Дані, що реєструють певну якість, якою наділений об'єкт, називаються якісними.
Якісні дані бувають двох типів:
\(1)\) порядкові, для яких існує порядок, що має змістовне значення;
\(2)\) номінальні, для яких немає змістовно інтерпретованого порядку.

Для обробки даних вимірювання використовують графічне, візуальне зображення наявної інформації. Добре відомий табличний спосіб задання функцій.
Дані таблиці можна зобразити за допомогою так званої гістограми частот і полігону.
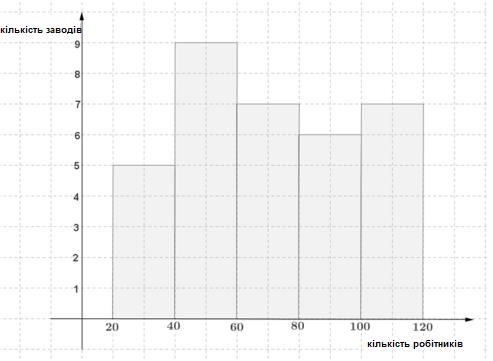
Гістограма частот — це фігура, що складається з прямокутників, які спираються на інтервали угруповання.
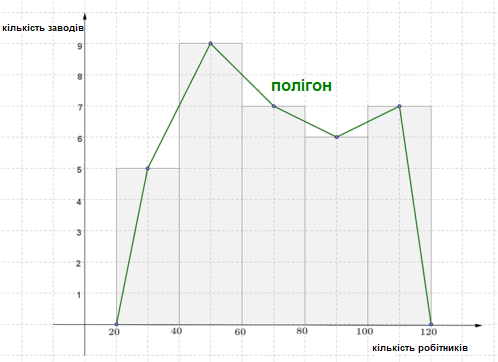
Полігон частот — один зі способів графічного зображення густини ймовірності випадкової величини. Полігон є ламаною, що сполучає точки, які відповідають серединним значенням інтервалів угруповання і частотам цих інтервалів.
Приклад:
У частотній таблиці відображено чисельність робітників на різних заводах.
Чисельність робітників | \(20-39\) | \(40-59\) | \(60-79\) | \(80-99\) | \(100-119\) |
Кількість заводів | \(5\) | \(9\) | \(7\) | \(6\) | \(7\) |
Гістограма частот:
Полігон частот: