Логарифмічна функція, її властивості і графік

Функцію, задану формулою

y = \log_{a} x

(a > 0, a \neq 1)

, називають логарифмічною функцією з основою $a$.

Основні властивості логарифмічної функції:

1. Область визначення логарифмічної функції — множина всіх додатних чисел.

D (f) = (0; + \infty)

;

2. Множина значень логарифмічної функції — множина $R$ всіх дійсних чисел.

E (f) = (- \infty; + \infty)

;

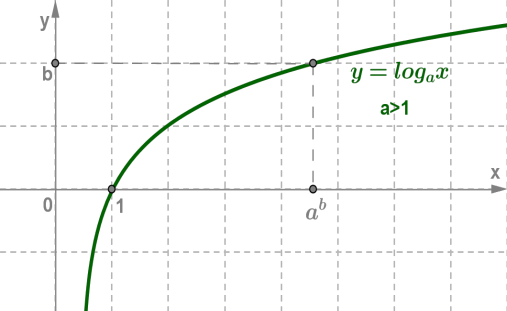
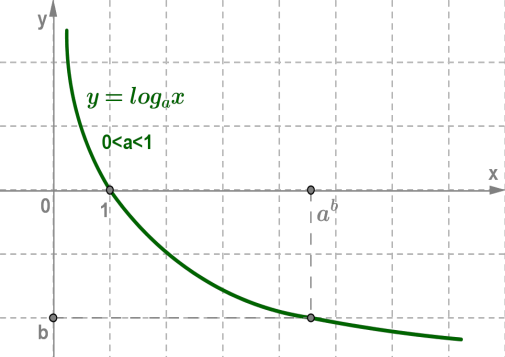
3. Логарифмічна функція на всій області визначення зростає при $a>1$, або спадає

при $0<a<1$.

Зверни увагу!

Логарифмічна функція не є ні парною, ні непарною;
не має ні найбільшого, ні найменшого значень;
не обмежена зверху, не обмежена знизу;

Графік будь-якої логарифмічною функції

y = \log_{a} x

проходить через точку $(1; 0)$.

Побудуємо графіки двох функцій

Приклад:

y = \log_{2} x

, основа $2>1$

$x$	$\frac{1}{4}$	$\frac{1}{2}$	$1$	$2$	$4$	$8$
$y = \log_{2} x$	$-2$	$-1$	$0$	$1$	$2$	$3$

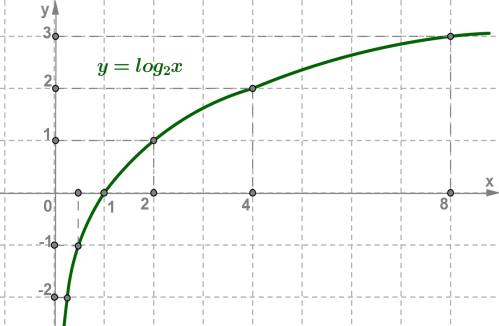
Приклад:

y = \log_{\frac{1}{3}} x

основа $0<$

\frac{1}{3}

$<1$

$x$	$9$	$3$	$1$	$\frac{1}{3}$	$\frac{1}{9}$
$y = \log_{\frac{1}{3}} x$	$-2$	$-1$	$0$	$1$	$2$

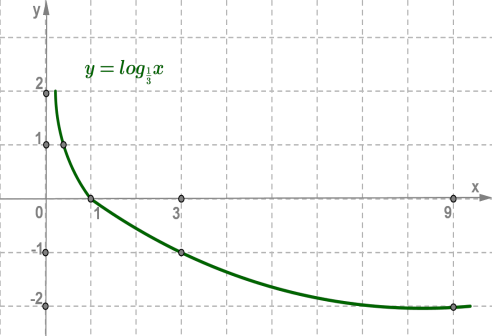
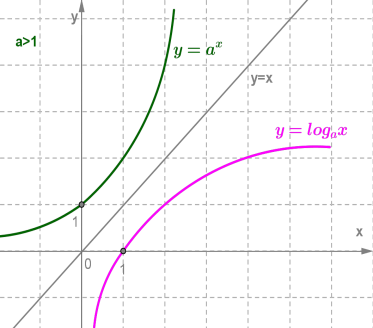
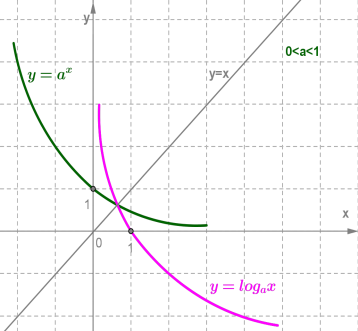
Логарифмічна функція

y = \log_{a} x

і показникова функція

y = a^{x}

, де

(a > 0, a \neq 1)

, взаємно обернені. Графіки цих функцій симетричні відносно прямої

y = x

Знайшли помилку?

\(x\)	$\frac{1}{4}$	$\frac{1}{2}$	\(1\)	\(2\)	\(4\)	\(8\)
$y = \log_{2} x$	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)

\(x\)	\(9\)	\(3\)	\(1\)	$\frac{1}{3}$	$\frac{1}{9}$
$y = \log_{\frac{1}{3}} x$	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)

1. Логарифмічна функція, її властивості і графік