Показниковими нерівностями називають нерівності вигляду ,
де - додатне число, відмінне від , і нерівності, що зводяться до цього вигляду.Нерівності розв'язуються за допомогою властивості зростання або спадання показникової функції:
- для зростаючої функції більшому значенню функції відповідає більше значення аргументу
- для спадної функції більшому значенню функції відповідає меньше значення аргументу.
Показникова функція зростає при
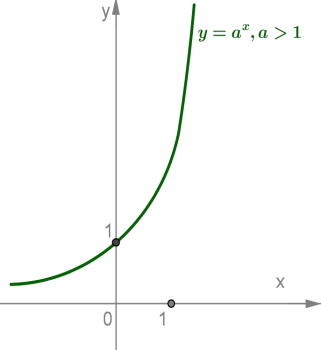
і спадає при
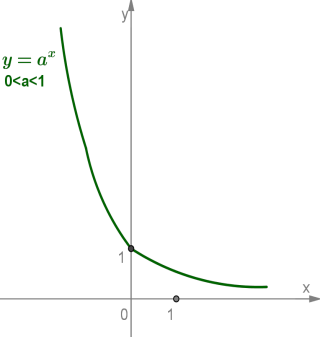
Показникова нерівність рівносильна нерівності того ж змісту , якщо
Приклад:
Розв'язати нерівність:
Маємо
Ця нерівність рівносильна нерівності того ж змісту , оскільки основа дорівнює 2>1 ( ),
звідки знаходимо .
Показникова нерівність рівносильна нерівності протилежного змісту , якщо .
Приклад:
Розв'язати нерівність:
Скориставшись тим, що , перепишемо задану нерівність у вигляді: .
Основою є число
Отже, розглянута нерівність рівносильна нерівності протилежного змісту ,
звідки знаходимо .