Розв'язанням рівняння з двома змінними \(p\) \((x; y)=0\) називають будь-яку пару чисел \((x;y),\) яка перетворює рівняння на правильну числову рівність.
Рівняння з двома змінними зазвичай має нескінченно багато розв'язків.
Приклад:
Рівняння задовольняє будь-яка пара \((x; y)\) — така, що точка координатної площини \(M(x; y)\) належить колу з радіусом \(3\) та центром у початку координат.
Якщо дано ціле раціональне рівняння з декількома змінними й цілочисельними коефіцієнтами і якщо поставлено завдання знайти його цілочисельні (або раціональні) розв'язки, то говорять, що задано діофантове рівняння.
Приклад:
Знайди цілочисельні розв'язки рівняння \(.\)
Виразимо \(x\) із даного рівняння:
При подільності числа \(y\) на \(3\) може бути три можливості:
\(1)\) \(y = 3k;\)
\(2)\) \(y = 3k+1;\)
\(3)\) \(y = 3k+2.\)
Якщо \(y = 3k,\) то отримаємо \(.\) Це число на \(3\) не ділиться, оскільки \(12k\) ділиться на \(3,\) а \(19\) — не ділиться.
Якщо \(y = 3k+1,\) то отримаємо \(.\) Це число на \(3\) ділиться.
Якщо \(y = 3k+2,\) то отримаємо \(.\) Це число на \(3\) не ділиться.
Отже, єдина можливість цілочисельного розв'язання рівняння — це пара чисел \((5-4k; 3k+1),\) де \(k\) — будь-яке ціле число.
Розв'язком нерівності \(p\) \((x; y)>0\) називають будь-яку пару чисел \((x; y),\) яка задовольняє цю нерівність, тобто перетворює її на правильну числову нерівність.
Приклад:
Розв'яжи нерівність: \(2x+3y>0\)
Побудуємо графік рівняння \(2x+3y=0\) — пряму.
Розв'язком нерівності є точки напівплощини вище або нижче від побудованої прямої.
Для правильного визначення потрібної напівплощини виберемо будь-яку точку з неї, координати якої підставимо в таку нерівність.
Для правильного визначення потрібної напівплощини виберемо будь-яку точку з неї, координати якої підставимо в таку нерівність.
Якщо нерівність буде правильною, то напівплощина вибрана правильно.
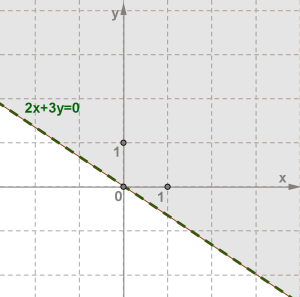
Вибравши контрольну точку \((1; 1)\) із верхньої напівплощини, отримаємо правильну числову нерівність:
Отже, розв'язком даної нерівності є верхня напівплощина.
Отже, розв'язком даної нерівності є верхня напівплощина.
Аналогічно можна міркувати при розв'язанні системи нерівностей із двома змінними.
Розв'язати систему нерівностей із двома змінними — означає знайти множину всіх таких точок координатної площини, координати яких задовольняють одночасно всі нерівності системи.
