Рівносильність нерівностей — урок. Алгебра, 11 клас.

Розв'язанням нерівності

f (x) > g (x)

називається будь-яке значення змінної \(x,\) яке перетворює задану нерівність зі змінною на правильну числову нерівність.

Дві нерівності з однією змінною

f (x) > g (x)

p (x) > h (x)

називаються рівносильними, якщо їхні розв'язки (тобто множини частинних розв'язків) збігаються.

Використання знака \(>\) непринципове, може бути будь-який інший знак нерівності.

Якщо розв'язок нерівності

f (x) > g (x)

\((1)\) міститься в розв'язку нерівності

p (x) > h (x)

\((2),\) то нерівність \((2)\) називають наслідком нерівності \((1).\)

Нерівність

x^{2} > 9

є наслідком нерівності

2 x > 6

\(.\) Дійсно, розв'язавши кожну нерівність, отримаємо:

\begin{array}{l} x^{2} - 9 > 0 \\ (x - 3) \cdot (x + 3) > 0 \\ x \in (- \infty; - 3) \cup (3; + \infty) \end{array}

\begin{array}{l} 2 x > 6 \\ x > 3 \\ x \in (3; + \infty) \end{array}

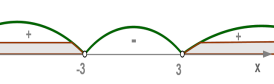
Розв'язок другої нерівності є частиною розв'язку першої, тому перша нерівність — наслідок другої нерівності.

Розв'язання нерівностей, що зустрічаються в шкільному курсі, ґрунтується на шести теоремах про рівносильність:

Теорема \(1\)

Якщо який-небудь член нерівності перенести з однієї частини нерівності в іншу з протилежним знаком, залишивши знак нерівності без зміни, то вийде нерівність, рівносильна даній.

Теорема \(2\)

Якщо обидві частини нерівності піднести до одного й того самого непарного степеня, залишивши знак нерівності без зміни, то вийде нерівність, рівносильна даній.

Теорема \(3\)

Показникова нерівність

a^{f (x)} > a^{g (x)}

рівносильна:

\(a)\) нерівності того самого змісту

f (x) > g (x)

\(,\) якщо \(a>1;\)

\(b)\) нерівності протилежного змісту

f (x) < g (x)

\(,\) якщо \(0<a<1.\)

Теорема \(4\)

\(a)\) якщо обидві частини нерівності

f (x) > g (x)

помножити на один і той самий вираз \(h(x),\) додатний при всіх \(x\) із області визначення (області допустимих значень змінної) нерівності

f (x) > g (x)

\(,\) залишивши при цьому знак нерівності без зміни, то вийде нерівність

f (x) \cdot h (x) > g (x) \cdot h (x)

\(,\) рівносильна даній.

\(b)\) якщо обидві частини нерівності

f (x) > g (x)

помножити на один і той самий вираз \(h(x),\) від'ємний при всіх \(x\) із області визначення нерівності

f (x) > g (x)

\(,\) змінивши при цьому знак нерівності на протилежний, то вийде нерівність

f (x) \cdot h (x) < g (x) \cdot h (x)

\(,\) рівносильна даній.

Теорема \(5\)

Якщо обидві частини нерівності

f (x) > g (x)

невід'ємні в області його визначення (в \(ОДЗ\)), то після піднесення обох частин нерівності до того самого парного степеня \(n\) вийде нерівність того самого змісту